in Extreme Events in Nature and Society, Frontiers Collection. New York/Berlin: Springer Verlag, November 2005. pp. 21-45
PDF
Abstract:
The urgency explicit in soliciting scientists to address the prediction of extreme events is understandable, but not really conducive to a foundational perspective. In the following methodological considerations, a perspective is submitted that builds upon the necessary representation of extreme events, either in mathematical or in computational terms. While only of limited functional nature, the semiotic methodology suggested is conducive to the basic questions of extreme events prediction: the dynamics of unfolding extreme events; the distinction between extreme events in the deterministic realm of physics and the non-deterministic realm of the living; the foundation of anticipation and the possibility of anticipatory computing; the holistic perspective. As opposed to case studies, this contribution is geared towards a model-based description that corresponds to the non-repetitive nature of extreme events. Therefore, it advances a complementary model of science focused on singularity corresponding to the non-deterministic understanding of high-complexity phenomena.
Keywords: representamen, sign process, time scale, reverse computation, anticipatory computing, causa finalis, holism.
The Representation of Extreme Events
Let us imagine that somehow we could fully capture an extreme event—earthquake, stock market crash, terrorist attack, epileptic seizure, tornado, massive oil spill, flood, an epidemic or any other occurrence deemed worthy of the qualifier “extreme.” What kind of measurements and other observations would qualify the result as complete shall remain unanswered for the time being. Based on what we know today—aware more than ever that “everything is in flux (“Panta rhei,” to quote Heraclitus [1])—and on the scientific model that presently guides knowledge acquisition, to fully capture an event (extreme or not)—i.e., to fully represent it—means not just to explain it, but also to ultimately be able to reproduce it. This is another way of saying that if we could adequately represent an extreme event, we would be able to predict it and similar events, as well as their consequences. Implicit in the fundamental perspective just sketched out is the expectation of determinism, a particular form of causality. More precisely, the representation contains the description of the cause or of the causal chain. Obviously this is no longer a case of simplistic representation of cause-and-effect, but one well informed by the realization that only the acknowledgement of a rich variety of causal mechanisms can explain the broad dynamics of complex phenomena. After all, the common denominator of extreme events is their complexity.
With all this in mind, let us denote the full description of an extreme event as its representamen, R. (The informed reader has already noticed that this unusual word comes from Charles S. Peirce [2].) There are no limitations to what R can be. It can be a record of quantities (numbers, i.e., the set N of natural numbers); it can be an event score (similar to a music score or to a detailed film script). Or it can be a completed computation—assuming that the algorithm/s behind the computation is/are tractable, that is, having a polynomial solution in the worst case. Or it can be a computation in progress, about to reach a halting stage, or reaching one in several generations (i.e., an evolutionary computation). Or it can be a combination of some or all of the above, plus anything else that science might come up with. Regardless of what R is and how it was obtained, if we could fully capture an event, we could also understand how the event—to be called henceforth object (and denoted O), for reasons of convenience—and its representation relate to each other (in other words how a change in R, the representamen, might affect a change in O, the event reproduced or anticipated). This understanding, whether by a human being, a scientific community, a computer program, or a neural network procedure—to be called I for interpretant process (according to the same Peircean terminology already alluded to)—is actually all that society expects from us as we dedicate out inquiry to extreme events. Indeed, we are commissioned (some explicitly, others implicitly) to conceive of methods for predicting extreme events. Based on such predictions, society hopes to avoid some of their consequences, or even for avoiding the event as such—let’s say a terrorist attack or an epileptic seizure.
The three entities introduced so far—R for representamen (the plural is representamina), O for object (to be defined in more detail), and I for interpretant—are derived from Peirce’s semiotics. For the scientist wary of any terminology that does not result from some specialization (such as the many mathematics branches growing on the trunk of mathema, the various theories of physics, the biological fields of inquiry such as molecular biology or genetics, and so on), a word of caution: Regard the entities introduced so far only as conceptual tools, and only in conjunction with the descriptions given so far. Actually, their relation can be conveniently diagrammed:

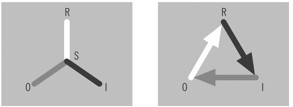
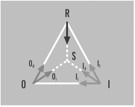
Fig. 1. A sign is something that stands to some one for some thing in some form or capacity (cf. C.S. Peirce, [3a, b, c]). The two diagrams represent two views: On the left, the sign as a structure S=S(O,R,I) and on the right, the sign as process that starts with a representation (R of O) to be interpreted in a sign process.
The diagrams tell a very clear story: “In signs, one sees an advantage for discovery that is greatest when they express the exact nature of a thing briefly and, as it were, picture it; then indeed, the labor of thought is wonderfully diminished,” (Leibniz as cited by Schneiderman [4] p. 185).
An unusual scientist, grounded in mathematics, astronomy, chemistry, logic, and geodesic science, Peirce considered natural phenomena, as well as social events, from a meta perspective. Indeed, semiotics is a meta-discipline, transcending all those partial representations that are the focus of the object sciences. This confers upon semiotics an epistemological status different from that of particular sciences. That is, it is a “science of sciences,” as Charles Morris [5] called it. Its generalizations in semiotic theory are not conducive to technological innovation as such, but rather guide the effort, such as in the design of user-computer interfaces, or the conception of languages, such as those used for programming or based on the DNA code. However, semiotic generalizations are extremely effective in assisting specialized research to maintain a reference outside the specialization pursued. They help scientists realize the relation between what is represented—in our case, extreme events—the representation—in whatever scientific theory and with whichever means (mathematical formulae, computer programs, etc.)—and the interpretation process associated with it. When many disciplinary and societal views are produced—as is certainly the case of this book and for which my contribution is conceived—we realize the need of a comprehensive trans-disciplinary framework that could guide the individuals involved in realizing the meaning of all the specialized views and methods advanced. An effective framework for further research in extreme events ought to facilitate integration of knowledge, as well as the conception of new means for knowledge dissemination leading to decision-making and action.
The formalisms associated with semiotics are varied. They are of logical origin. In the late 1970s, I worked on a mathematical formulation of semiotic operations [Nadin, 6]. Animated by his interest in Peirce’s sign classes, Robert Marty [7, 8, 9] pursued a similar goal. Joseph Goguen [10] finally worked towards the explicit goal of an algebraic semiotics, facilitating applied work. Neither of us considered that interest in the study of extreme events might benefit from semiotics, formalized or not. But in the final analysis, what brought up the semiotic perspective in these introductory lines is the broad motivation of our effort: how to make semiotics useful beyond the contemplative dimension of every theory. One avenue, as it now turns out, is the path towards the foundation of anticipation, the anticipation of extreme events, in particular.
From Signs to Anticipation
Let me quote from the Introduction to the report of the workshop entitled Extreme Events. Developing a Research Agenda for the 21st Century [11]:

It is no overstatement to suggest that humanity’s future will be shaped by its capacity to anticipate [italics mine], prepare for, respond to, and, when possible, even prevent extreme events.

The notions of anticipation and of the sign are coextensive. Representations come into existence as the living—from the simplest level (monocell) to the most complex known to us (the human being)—act. Vittorio Gallese [12] brings proof that acting and perceiving cannot be effectively distinguished. He starts with an obvious example: the difficult task of reducing one’s heartbeat is made easier once a representation—an electrocardiogram in real time—is made available to the subject. Indeed, biofeedback provides an efficient way of controlling a given variable (heart rhythm, in the example mentioned, cf. p. 29).
Representations, which are the subject of semiotics, are relational instruments. Every human action—and for that matter, every action in what is called the living—is goal driven. Gallese reports on single-neuron recordings in the premotor cortex of behaving monkeys. What drives the neurons is the goal of the action. He states:

“To observe objects is therefore equivalent to automatically evoking the most suitable motor program required to interact with them. Looking at objects means to unconsciously ‘simulate’ a potential action. In other words, the object representation is transiently integrated with the action-simulation,” [p. 31].

Quite some time before Gallese’s experiments, my own elaborations [Nadin, 13] on what drives the human being—the actions through which they self-constitute, that is, their pragmatics (we are what we do, no more, no less)—made a point that is the fundamental thesis of this article.
Thesis 1: Extreme events should be qualified in relation to how they affect human life and work. Let me explain: Extreme events, regardless of their specific nature, are not simply acknowledged by virtue of their syntax: the formal characteristics as we read them on various recordings of seismic activity, brain activity, wind direction and intensity, etc. Extreme events are not reducible to the semantics defining them as such; the label applied in the form of categories of hurricane, or of assigned seismic intensity on a standardized scale, or of a seizure type, for example. The defining quantifier regards how they affect human activity, i.e., the pragmatics of existence.
It is the dynamic relation between the event and those experiencing it (directly or through some form of mediation) that counts. Moreover, the plurality of relations, corresponding to the various ways in which we interact with the world in which we constitute our identity, is what interests us. That we can quantify the effects of extreme events (in the number of lost lives, in the costs of preparation, recovery, and damaged infrastructure, in ecological impact, etc.) does not mean that the numbers represent the impact of the event. Human life and activity are subject not only to quantity descriptions, but also to deep quality consequences.
What guides the exposition so far is the realization that while everyone wants to anticipate, or at least somehow, even in a limited way, to predict extreme events, no one steps forward to remind us of Gödel’s warning [14] that we can at best expect partial results: a complex system cannot be described at the same time in a complete and consistent manner. As a theorem in formal logic, it has often been misinterpreted. What brings it up here is the methodological need to find out to which extent it predicts the necessary failure of all attempts to anticipate extreme events, or only suggests that we need to consider ways to segment, to partition, the various aspects of extreme events and concentrate on partial representations (cf. Fig. 2).

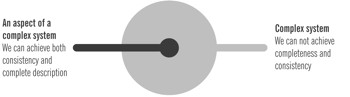
Fig. 2. Consistency and completeness are complementary. In order to circumvent the intrinsic characteristic of complex systems, we can focus on partitioned aspects. The challenge is to perform an adequate partitioning.
Descartes Rehabilitated
Seen from this perspective Descartes’ reductionism and determinism—the foundation of humankind’s enormous scientific and technological progress in the last 400 years—makes more sense than his critics would like to credit him with. The question of whether Descartes knew well ahead of Gödel that complex systems are impossible to handle in their entirety, or he only asked himself (obviously in the jargon of the time) how we can reduce complexity without compromising the entire effort of knowing will never be unequivocally answered. What we do know is that reductionism and determinism operate in a major section of perceived reality: Everything there is (i.e., reality) is reduced to that subset of reality that constitutes the subject of physics. And everything that functions, including the living—minus the human being, for religious reasons that had more to do with Descartes’ caution than with scientific reasoning—is seen as equivalent to a machine. That Descartes’ understanding of the physical world and our current understanding of physics are quite different needs no elaboration. Science advanced our understanding of determinism and causality in ways that at times appear as counter-intuitive. Think of the quantum mechanics description of the microcosm. Think of the dynamic systems models in which self-organization, among other dynamic characteristics, plays an important role in maintaining the system’s coherence. Hence, it would be unwise not to distinguish between
a) extreme events in the realm of the physical world—for which the science inspired by the Cartesian model is, if not entirely adequate, the best we have—and
b) extreme events in the living—for which the Cartesian perspective is only partially relevant.
Time, Clocks, Rhythms
If the representation of an extreme event as a representamen R were possible, it would necessarily involve a time dimension. After Descartes, time was associated with the simplest machine of his age—the pendulum clock—and reduced to interval. If not Descartes, then at least some of his contemporaries already knew that to associate gravity to rhythm is convenient, but not unproblematic. At the pole (north or south), time in this embodiment is quite different from time in Paris or in Dallas, Texas. And on a satellite, depending upon its orbit, it is a different time again. The problem was addressed as we adopted oscillations (mechanical, as in clocks and watches, or atomic) and resonance as a “time machine,” and then declared a standard—that of the cesium atom—easy to maintain and to reference. But with Einstein and relativity theory, we came to realize that the “atomic clock” is a good reference as long as it is not subjected to a trip on a fast-moving carrier. Some physical phenomena take place along a timeline for which the day-and-night cycle in the western hemisphere, or the pendulum’s gravity-driven rhythm, is either too fine-grained (think about cycles of millions of years), or too coarse (fast processes at nanoseconds and below scale). Even more dramatic is our realization that within the living, many different clocks operate at the same time, and many synchronization mechanisms can be noticed. If they are affected, the system can undergo extreme changes. It turns out that the linear representation of time, through an irreversible vector, is a useful procedure as long as the time it describes is relatively uniform and scale independent. But time is neither uniform nor independent of the frame of reference.
Once we ask what it would take for the representamen R of an extreme event to become a complete, effective description of the event, we implicitly ask what it would take to anticipate it. Indeed, a complete description can be fully predictive only if it makes a time difference mechanism possible:
Event (E) as a time function t_E
Prediction (P) as a time function t_p
Evidently, the two times t_E and t_p are not identical: t_E ≠ t_p. Moreover, t_p has to be faster than t_E in order to allow for the possibility of prediction or anticipation.
An anticipatory system is a system whose current state depends not only on a previous state, but also on future states (cf. Rosen [15], Nadin [16]. As opposed to a predictive mechanism that infers probabilistically from the past, an anticipatory procedure integrates past experiences, but weighs them against possible future realizations. One of the better-known operative definitions of an anticipatory system is: “An anticipatory system is a system that contains a model of itself unfolding in faster than real time,” [17]. What this description says is that simulations are the low end of anticipation. What it does not say is that although within physical systems (machines, in particular) we can execute different operations (for instance, computations) in parallel, and even some operations (computations) faster than others, without a mechanism for interpreting the meaning of the difference between “real-time” operations (computation) and “faster than real-time” operations (computations), we still do not have an effective anticipatory mechanism. Indeed, only the understanding of the difference in outcome between so-called real-time and faster-than-real-time operations can afford anticipation. Two conditions must be fulfilled:
a) the effective model should be complete;
b) an effective mechanism for discrimination between the process and its model has to be implemented.
Some would argue that the model does not have to be complete (or that it cannot be complete). If this were true, we could as well make the conception of the incomplete but still useful model the task of predicting, as though we knew which part of the dynamics of the system is more relevant than what is left out. Others argue that all it takes is some intelligence in order to understand the meaning of the difference. From all we know so far in dealing with anticipation and the human being, intelligence is marginal, if it plays any role at all. Let us take classical some examples.
Anticipation of moving stimuli (cf. Berry et al [18]) is recorded in the form of spike trains of many ganglion cells in the retina. The facial action coding system (cf. Ekman and Friesen [19]) is a record of “character” that we spontaneously “read” as we perceive faces in some unusual situations (the trusting hand extended when there is need). Proactive understanding of surprising events is the result of associative cognitive activity (cf. Fletcher et al [20]. More recently, Ishida and Sawada [21] confirmed that the hand motion precedes the target motion. (Remember when you last caught a falling object before you “saw” it?) Intelligence is not traceable in the process or in the quantitative observations. As a matter of fact, high performance anticipation—e.g., ski, tennis, hockey, soccer—is not associated with a high IQ or with any other feature of intelligence. What is identifiable is learning—and implicitly the dimension of training anticipatory attributes—but of a precise type. It is not explanatory learning; it is rather procedural, internalized rather than externalized.
In view of this, a representamen R of an extreme event understood as its full operational description makes sense only in association with an interpretant process I. This itself can be conceived as a machine that is context sensitive and able to learn. As the representamen unfolds in a never-ending prediction sequence, the interpretant not only relates it to the extreme event it captured, but also to other events as they take place in the world. In order to achieve this dynamic behavior, it has to be conceived as a distributed computation, actually as a grid process that takes as input the knowledge acquired so far (representamen) as well as the new knowledge resulting from the representation of extreme events taking place in real time. And even in this possible implementation, the interpretant process will not be more than a surrogate to a living interpretant process.
The Hybrid Solution
Thesis 2: Since the living is not reducible to a machine, our best chance of understanding our own knowledge regarding extreme events, and thus provide for effective anticipation, are hybrid systems that integrate the human being.
I am aware that this thesis runs counter to the dominant expectation of fully automated anticipation, or at least prediction. Although we deplore the enormous cost of the consequences of extreme events—often including death and bodily impairment, disease and suffering—we are, so it seems, not willing to realize that the most expensive machinery imaginable today will not fully replace interaction of minds (cf. Nadin [22] as a component of the interpretant process. Our obsession is still with the interaction (cf. Fig. 3), in particular, human-machine interface.

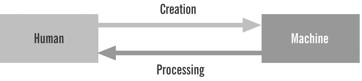
Fig. 3. Human-Machine interaction. The process is intensely asymmetric/asynchronic.
This focus is not unjustified to the extent we entertain the illusion that machines will eventually carry out any and every form of human activity. After all, Minsky [23] was not alone in stating that

“In from three to eight years, we will have a machine with the general intelligence of an average human being. I mean a machine that will be able to read Shakespeare, grease a car, play office politics, tell a joke, have a fight. At that point, the machine will begin to educate itself with fantastic speed. In a few months, it will be at genius level, and a few months after that, its power will be incalculable.”

Despite this reductionist-mechanistic viewpoint, we are now discovering that given the continuous diversification of human activity, the machine is bound to be at least one step behind human discovery: It does not articulate questions. Expressed in other words, we are discovering new ways through which we can increase the efficiency of our efforts (physical, mental, emotional). Therefore, the logical alternative is not to transfer human functions and capabilities to machines, but to provide for an alternative model: the integration of the human being and the machine. What results is a very complex entity, ultimately characterized by its degree of integration. Instead of limiting ourselves to the human machine interaction, we should concentrate on the very complex entity that results from integration (cf. Fig. 4).

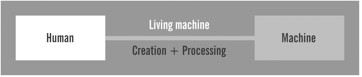
Fig. 4. The “Human-Machine” living machine.
Let us contemplate simple examples of implementation:
a) The “mind” driving the machine (cf. the experiments, so far with monkeys, [24]), thus avoiding the “bottleneck” of current user interfaces, notoriously asynchronic. We know that a lot comes out of machines, but very little—mainly interrupt commands—go from user to machine.
b) The coupling of the non-deterministic informational space “state-of-the-human” (many parameters, with heterogenous data types such as temperature, color, pressure, rhythm, etc.) with the deterministic machine state—such as in hybrid control mechanisms. The data bus in the machine part is connected to the “living bus”—rich learning and forgetting affect interaction between the human and the machine.
These examples reflect the “state of the art” currently reached. If we could further integrate the living (not only human) and a machine endowed with pseudo-living properties (such as evolutionary programs), we would be better positioned to achieve a semiotic machine in the proper sense of the expression, and thus to expect anticipatory characteristics augmented by computation.
Let us revisit the introductory hypothesis: the possibility of achieving a full record of an extreme event. We denoted the extreme event as object O without considering its condition. In reality, an extreme event appears to us—as we are part of it, experiencing it—as an immediate object: the meteorologist is inundated with data from trackers, radar readings, and sensor information. (Similar readings are made by a physician examining a patient who might have an epileptic seizure; or by seismologists as they consider issuing a warning of a catastrophic earthquake that would require massive emergency measures.) The immediate object O_i, which can be characterized through rich data, is only suggestive, but not fully indicative, of the dynamic object. After all, the tornado might not take place, despite all the readings; the seizure might not occur, or might take a mild form, indistinguishable from normal brain activity; or the seismic wave might be ambiguous.
Associated to the immediate object O_i is the immediate, although at times less than precise, understanding of what the description (representamen) conveys, i.e., the immediate interpretant I_i. Most of the time, i.e., in all we call prediction (including forecast), this understanding is based on previous experience, that is, on probabilities. For example, in the past, a radar echo and a triple point on a surface chart suggested tornados. The dynamic interpretant I_d, not unlike a neural networks propagation, corresponds to inferences from what is apparent to what might happen—to the space of possibilities. This consists of all that can happen (i.e., what is associated with meteorology data such as weak shear, moisture, stationary front in vicinity). Integrating the probabilistic and the possibilistic dimensions of extreme event forecast is the final interpretant I_f: “If you haven’t thought about it before it develops, you probably won’t recognize it when it does.” This comes from a professional in weather forecasting, Charles A. Doswell, III, as reported by Quoetone and Huckabee [25]. The transcripts of the various conversations among traffic controllers, airline representatives, and the military personnel in charge of guarding USA air space during the events surrounding the terrorist attacks of what has come to be known as 9/11 clearly reveal that nobody thought about the possibility of an operation at the scale of and with the means conceived by the terrorists. The diagram given below captures the intricate relation (corresponding to a triadic-trichotomic sign relation) of the entities under consideration:

By no accident, the infatuation with the sign originates in medicine, more precisely, in the practical endeavor known as diagnostics. But the “symptoms” of extreme events (also known as the foretelling signals, whether in seismology, meteorology, medicine, terrorist activity, market analysis, etc.) point to a very complex sign process. The triadic-trichotomic representation of the sign suggests the need to distinguish between the appearance (immediate object O_i) and the evolving object of our attention (dynamic object O_d) It also makes us aware that the process of interpretation starts with the perception of appearance (I_i) and continues with the formulation of a theory (I_f), which in turn can be further interpreted (the state of knowledge regarding an extreme events at some moment in time). Quite often, we examine a representamen R as a symptom (let’s say seismogram, or some representative data pertinent to physical events) and infer from symptoms to possibilities, that is, a quantified record of what can be expected.
Extreme events are notorious for casting doubt on forecast verification statistics. Due to the nonlinearities characteristic of extreme events, random factors lead to an ever increasing difference between the statistically driven prediction and the observed event. Combining probabilistic and possibilistic descriptions opens new modeling perspectives. The fact that probability and possibility are not independent of each other (nothing can be probable unless it is possible, and not every possibility can be associated with a probability before an event) makes the task even more difficult. Since in respect to probability a vast body of literature is available, I will make short reference to possibility distributions.
Actually, we know that there is no “generally accepted formula for the mean of uncertainty or ignorance induced by a possibility distribution” (cf. Guiasu [26] p. 655). The best that, to my knowledge, has been proposed so far is an E-possibilistic entropy measure.
If Α = {α1, . . . αk} is a set of outcomes (let’s say, the effects of an earthquake, or of a storm) within boundaries, and Π = {Ï€1, . . . Ï€k } is a possibility distribution on Α, with Ï€i ≤ 1, i=1, . . . k, the measure of uncertainty (or ignorance) is the optimal value of the nonlinear equation:

subject to limitations:

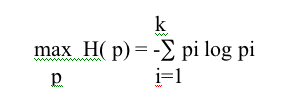
Indeed, we are always informed, at least partially, about what has already happened; but we are ignorant in respect to what might happen (the possible event). The measure of our ignorance is always dependent on how well defined the possibility space is. The consequences for which α_i stands are hypothetical, sometimes (such as in financial crashes) affected by the perception of those involved (the investors), but usually not obviously dependent upon their activities. A house constructed in the vicinity of a fault line does not augment the intensity of the earthquake—should one take place—but the impact (human, social, economic, etc.). The possibility distribution is therefore a representation of the various correlations expressed in the extreme event. No possibilistic entropy depends only on the possibility distribution. Together with probability considerations, these intricate relations are implicit in the R expression and are indicative of both extreme events in the physical and in the living.
We ought to realize that these entities (R, O, I) are not abstractions, but a logical guide to constructing an effective system of anticipation. Accordingly, we need to proceed by giving life to this diagram, such as in specifying the relation between the data and the possibility distribution. We also need to define all its components, and furthermore, to proceed with a semiotic calculus that will generate an anticipatory self-mapping system. To give just one example: Let us define an extreme event as an expression of dynamics. (“Expression” is used here in analogy to gene expression.) If we accumulate data—meteorological, geological, brain activity, financial market transactions, for example, each associated with a possible extreme event—our goal would be to extract from the representamen R patterns of expression (i.e., patterns of dynamics, which means patterns of change) inherent in the data. Mathematical techniques for identifying underlying patterns in complex data (i.e., in complex representamina) have already been developed for object recognition by computer-supported vision systems, for phoneme identification in speech processing, for bandwidth compression in electrocardiography and sleep research. These are clustering techniques (hierarchic, Bayesian, possibilistic, etc.). Among these techniques, the so-called self-organizing maps (SOM) correspond to a semiotic self-mapping. They involve a high number of iterations. In the final analysis, an SOM is associated with a grid. A rectangular grid begs the analogy to an entomologist’s drawer (adjacent compartments hold similar insects), or to a philatelic collection (adjacent pages in the album hold similar stamps). The SOM of a possible extreme event is nothing but the representation of all the “insects” or “stamps” not yet collected, or even of the “stamps” not yet printed. For an iteration i, the position of a variable V_e is denoted as f_i(V_E). The formula

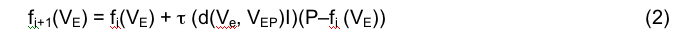
describes the next position of the extreme event variable considered. Learning is involved in the process (Ï„ is the learning rate); and there is randomness (to replace the living component). In such a procedure, semiotic considerations are no longer meta-statements, but become operational.
Human beings operate naturally in the semiotic realm. They generate cognitive maps as they act in relation to the extreme event variable. These mental maps guide our actions. Even the influence of predictions and forecasts affect these self-generated maps. We do not process chairs or electrons or thunder in our minds, but rather their representamina. Accordingly, a semiotic machine combines the perception of signs with the production of signs (cf. Fig. 6):

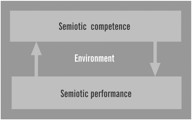
What the diagram suggests is that the human being’s self-constitution (i.e., how we become what we are through what we do) implies the unity of action—driving our perception of the world—and reflection. Therefore, to do something, such as to deal with extreme events—reflect upon, cope with their impact, predict them, etc.—actually means to anticipate the consequences of our actions. In effect, this translates neither into an anticipation method nor into specific means, but rather into the realization that anticipation is an evolution immanent characteristic. Should we ever be able to build an evolutionary machine—that is, create a living entity—it will have to display anticipatory characteristics. For all it’s worth, the realization that anticipation is an evolution immanent characteristic means that anticipation of extreme events is possible, but not guaranteed. Evolution itself is not a contract with nature for individual survival or survival of the species. The extreme events that led to the extinction of the dinosaurs is only one example among many others.
If instead of considering the R of a natural extreme event (earthquake and the like) we look at the plans on whose basis the A-bomb was built, or chemical and biological weapons are produced, or the new “smart” weapons (producing targeted extreme events!), we still remain in the semiotic realm. The R_A (for atomic bomb), or the R_C (for some chemical weapon), or the R_B (for biological weapons), or the R_S (for smart weapons) are an effective description of a potential extreme event, which we can fully predict within an acceptable margin of error. Bombing the desert (which used to be called “nuclear testing”) is quite different from bombing a populated area. In respect to R_C or R_B, and even R_S, we can as well, within other margins of error, predict what might happen. The extreme event (O)—the unity between O_i and O_d, i.e., the appearance and the dynamic unfolding of the event—thus “contained” in the description (R) becomes subject to a process of interpretation. This extends from scientific analysis and planning, to engineering and testing, as well as to media reports, fiction, and movies, not to mention the production of interpretations, true and false, of secret services intent on confusing the potential users of such devices. Indeed, extreme events, whether natural or artificial, become part of the political experience, and thus their prediction impacts politics also. Extreme events lead to a whole bureaucracy (emergency funds set up to meet needs), and to new laws (including ones meant to prevent market crashes or terrorist attacks).
It has often been remarked that social systems (and for that matter, systems pertinent to living communities, human or not) display anticipation. The less constrained a system is, the higher its resiliency. Meaning comes into existence with hindsight: “What happened to the subway that came to a screeching halt?” “What does it mean that an airplane hit a skyscraper?” What does it mean that someone has a seizure?” A logistic map can inform us about a direction of change. Market processes exemplify the process. Feedback and feedforward work together; production, supply, demand, and all other factors are underlying factors in market dynamics. A crash—an extreme event—is not dependent upon the anticipatory actions of informed or uninformed individuals, but rather upon aggregate behavior. Cellular automata able to operate on two different time scales (real time vs. faster than real time) could, in principle, capture the recursive nature of those who make up the market.
But in real life (whatever that means), we can act only in the present (as events are triggered). As such, the interpretant process for which a cellular automaton stands appears to us as a funnel:

The immediate object (the extreme event) unfolds in the huge space of possibilities that one can conceive of and pursue systematically. To be successfully anticipatory means to progressively reduce this space until the convergence of the open cone-shaped object.
Can a Computer Simulate Anticipation?
In effect, to anticipate is to move along the time vector from the event (tornado, flood, seizure, etc.)—the neck of the funnel—as it unfolded, to its initial conditions. In the language of dynamic systems, this means to move from the strange attractors embodying the extreme event to the conditions feeding the dynamics of the system.

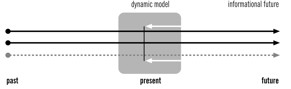
Nonlinear processes affect the “edges” of the dynamic distribution (e.g., how wide a swing a stock market can take, what the extreme temperatures are, what the atmospheric pressure values are, what the seismic parameters are, the level at which a system’s stability is affected). But there is no indication whatsoever that these processes display any regularity.
Scientists such as Sornette, Helbing, and Lehnertz—to name three among those published in this volume—are very dedicated to this approach. For instance, Sornette is well respected for considering self-organized criticality and out-of-equilibrium conditions. He advanced the hypothesis that extreme events are due to the system’s endogenous self-organization. In contrast to prevailing views, he covers a very large area of public interest (from geological aspects to the future of humankind on earth). The abstraction in Helbing’s model of collective behavior goes back to self-driven many-particle systems. Malfunctions in the form of abnormal synchronization of a large number of neurons catch the attention of those (such as Lehnertz) looking for the prediction potential of apparati (such as the multi-channel EEC recording) if the appropriate determination of the abnormality, detected through statistical evaluation, is performed.
Each time they, and others who follow a similar physics-driven path to discovery, come upon patterns in the data subject to their examinations, they pursue the thought of identifying regularities that can ultimately justify prediction. Some are on record—a very courageous scientific attitude—with predictions (regarding, e.g., the economy, financial markets) that the public can evaluate. Others have commercialized their observations (e.g., regarding crowd behavior). It would be out of character and out of question for me to try to shed doubt on models mentioned here for their elegance and innovation. But the reader already knows where I stand epistemologically. And given this stand, I can only suggest that, for the particular aspects on which my colleagues focus, acceptable predictions are possible. What is not possible is a good discrimination procedure, one that allows us to compare, ahead of the future, between good and bad, appropriate and inappropriate predictions. For the past, which they assume to be repeated in some form or shape, the prediction is usually good (or at least acceptable). But once complexities increase, even within the physical, the extreme event starts to look like a “living” monster. We cannot afford to ignore this fact.
This journey from the extreme event states to the states leading to it is, for all practical purposes, a reverse computation (regardless of whether the computer implementation is in silicon, DNA, quantum states, etc.). In Richard Feynman’s words [27], this is equivalent to asking, “Can a computer simulate physics exactly?” Reversibility is in fact the characteristic of a computation in which each step can be executed and unexecuted. Making and unmaking an omelet is only a suggestive way of explaining what we refer to. Take it at the scale of an earthquake and imagine the weird computation of the earthquake as output, and its reverse. But even at the scale of an epileptic seizure or financial crash, the film played in reverse is not easy to conceptualize—and not at all clear whether at all feasible.
That physical laws are generally reversible automatically provides for a reversible computer (with all the costs associated to erasure of information). But what is not clear is whether an earthquake, a heart attack, a tornado, or a seizure is the result of a deterministic process, or at least one of deeper levels of order. If the computation of an earthquake were of the condition of the process leading to the earthquake—that is, if one could define an “earthquake machine”—we would probably profit from the reversibility of the computation. It is very exciting to compute in the medium we examine, provided that we examine events of regular nature (no mater how deep the regularity is hidden). But not unlike the infinite interpretant process characteristic of semiotics—each interpretation becomes a new sign, ad infinitum—extreme events seem either unique (irreducible to anything else) or only an instance of a longer development that goes beyond what we call tractable.
A New Equilibrium
Third thesis: Extreme events are actually the preliminary phase leading to a necessary new state of balance leading to the next extreme event (cf. Fig. 9).

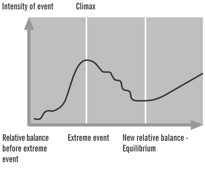
What I am saying is that the epileptic seizure is, in its own way, a process that preserves life, since it leads to the post-seizure condition that replaces the endangering state prior to it. Or, that the earthquake—a tremendous energetic peak—ends up in the post-quake condition of relative energetic balance, and of infinitely less destructive potential earthquake. Otherwise, the potential future event would grow and grow until the earthquake’s “resources” are exhausted. With this in mind, I suggest here that we are dealing with what physics has stubbornly rejected for the sake of homogeneity and determinism: the causa finalis as the necessary path of dynamic unfolding.
Aristotle distinguished among four categories of causation: material cause, formal cause, efficient cause, and final cause. In contemporary jargon, they correspond to different kinds of information. If we apply these categories to a house, it is evident that materials—cement, brick, wood, nails, etc.—pertain to the material cause. Builders (think about the many types of workers involved in excavating, mixing and pouring concrete, bricklaying, etc.) make the efficient cause clear through their work, while the plans they go by (blueprints and various regulations) represent the formal cause. The final cause is clear and simple: Someone needs or wants to live in such an edifice.
Now take a work of art. Materials, the work of an author, and the various sketches are well defined. But who needed or wanted the work? (Who needs or wants an extreme event?) In some cases, there is one person who acted as commissioner. In the majority of cases, the action (make the art work) is driven by the artist dedicated to expressing himself or herself, to ascertaining a view or perspective, to unveiling an aspect of reality unknown to others or perceived in a non-artistic way. The final cause is the work itself, as it justifies itself to itself within a culture and within a social context. The pragmatics of art is the answer to the “Why?” of a work of art, not to the “How?” (which pertains to its efficient cause). As science eliminated the legitimacy of anything even slightly related to causa finalis, it raised the infatuation with “How?” to the detriment of the question essential to any artistic experience: “Why?” Indeed, the “Why?” of an extreme event should interest us at least as much as the “How?” if we want to get closer to prediction, not to say to anticipation of extreme events.
It is less suspicious to affirm such an idea today now that bifurcations and attractors were introduced into scientific jargon (cf. Feigenbaum, et al [28]). The equilibrium following extreme events makes us aware of the variety of ways in which the physical substratum of all there is, is preserved through infinite processes. However—and this goes back to the major distinction I have advanced so far—extreme events in the physical universe compared to extreme events in the living are subject to predictive actions only to the extent that a pre- and a post-phase are identifiable. In this sense, time appears as a component of life, not just as one of its descriptions.
This prompts the next thesis of this article. Fourth thesis: The action of anticipation cannot be distinguished from the perception of the anticipated.
This applies in particular to extreme events as episodes in the self-constitution of the living, of the human being in particular. Testimony from folklore and anthropological evidence make us aware of the variety of anticipatory behavior of the living (animals, insects, reptiles, plants, bacteria) in relation to extreme events. This evidence has always been subjected to scientific scrutiny: Can it be that in some cultures important information regarding extreme events (earthquakes, floods, seizures, epidemics, etc.) has been derived from the interpretation of animal behavior and characteristics by the people sharing the environment with them? And if so, can we derive from this information anything useful for predictions of extreme events. After all, the living is endowed with anticipation, and accordingly, the anticipation of extreme events in the natural realm cannot be excluded. Moreover, there is sufficient anecdotal evidence to suggest that epileptic seizures in humans are signaled ahead of time by dogs. Similar anecdotal reports are often mentioned even in scientific publications.
As non-natural factors—such as anthropogenic forces related to urban development, land conversion, water diversion, pollution—increasingly affect the environment, animals, birds, plants, etc. exhibit new patterns of behavior. Even these changes are indicative of the tight connection among all components of the ecosphere. Ecological consequences of extreme events are rapidly becoming the focus of many scientists who realize the need for a holistic approach (cf. British Ecological Society [29]). We are losing important sources of information as we create artificial circumstances for nonlinearities that, instead of eliminating the risks associated with extreme events, actually increase their impact, and sometimes their probability and possibility. Numerous dams that marginally adequate to function under extreme weather conditions have made us aware of the extreme event potential their failure can entail. Buildings of all types, devices we place on mountains or under water, satellites circling the earth—they have all amplified the possibility space of extreme events. The possibility to hit skyscrapers with airplanes did not exist before we started to fly using “mechanical birds,” and built high to the sky. In this context, interestingly enough, we are forcing nature (and ourselves) towards machine behavior. Farms become food factories; workers are expected to act like machines; institutions become machines with specialized functions (e.g., doctors as “human body mechanics,” hospitals as spare parts factories, the state as a machine for maintaining the coherence of the social system, police as machines for maintaining order). The expectation is regularity, and all the measures undertaken worldwide following 9/11 are meant to ensure the highest predictability of the irregular (including the extreme events subject to the scrutiny of Homeland Security).
This expectation is fed by a scientific model of prediction and reproducibility corresponding to the world of physics. Indeed, to drop a stone from the same position, under the same circumstances (humidity, wind) will always produce the same measurements (of speed, position at any moment in time, impact upon landing, etc.). It is a predictable experiment; it is reproducible. Even if we change the topology of the landing surface, the outcome does not change.

Let a cat fall and derive the pertinent knowledge from the experiment. This is no longer a reproducible event. The outcome varies a great deal, not the least from one hour to another, or if the landing topology changes. The stone will never get tired, annoyed, or excited by the exercise.
Applied differential geometry allows for the approximate description of an object flipping itself right side up, even though its angular momentum is zero. In order to accomplish that, it changes shape (no stone changes shape in the air). In terms of gauge theory, the shape-space of a principal SO(3)- bundle, and the statement, “Angular momentum equals zero,” defines a connection on this bundle [30]. The particular movement of paws and tail conserves the zero angular momentum. The final upright state has the same value. This is the “geometric phase effect,” or monodrony. Heisenberg’s [31] mathematics suggests that, although such descriptions are particularly accurate, we are, in observing the falling of a cat, not isolated viewers, but co-producers of the event. The coherence of the process, not unlike the coherence of the apparently incoherent class of events we call extreme, is the major characteristic.

Fig. 11. The cat never falls the same way.
This is where the need to consider the living as different from the inanimate physical becomes more obvious. In order to address this, I will make reference to the work of an established physicist, Walter Elsasser—who worked in quantum mechanics (with Niels Bohr) and was very familiar with Heisenberg. He dedicated the second part of his academic career to a scientific foundation of biology. These considerations are appropriate in this context if the fundamental distinction between extreme events physical in nature and extreme events peculiar to the living should effectively be pursued. They can guide us further if we realize that there is more than a one-way interaction between extreme events as they emerge, and our perception. We are not just spectators at a performance (sometimes scary), but also, in many ways, co-producers.
A Holistic View
A physicist of distinguished reputation, Walter Elsasser [32] became very interested in the living from an epistemological perspective. As in Rosen’s case—Rosen being the mathematician most dedicated to the attempt to understand what life is—it would be an illusion at best to think that we could satisfactorily summarize Elsasser’s attempt to reconcile physics with what he correctly perceived as a necessary theory of organisms. Rosen and Elsasser had the focus on complexity in common. But as opposed to Rosen, Elsasser was willing to pay his dues to the scientific matrix within which he found his own way: “The successful modern advance of reductionism rests on certain presuppositions which at this time are no longer questioned by any serious scientist.” Moreover, and here I quote again, “There is no evidence whatever that the laws of quantum mechanics are ever wrong or stand in need of modification when applied to living organisms.” All this sounds quite dogmatic and, for those versed in science theory, almost trivial given the fact that theories are ultimately coherent cognitive constructs, not continents waiting to be discovered. Physics, in its succeeding expressions, is no exception. For the reader not willing to delve into the depths of the argumentation, the position mentioned is not really inspiring. Opportunistically, and as Rosen did as well, he refutes vitalism, “the idea that the laws of nature [that is, physics] need to be modified in organisms as compared to inanimate nature.” Serious scientists in all fields and of all orientations have discarded vitalism, just as alchemy was discarded centuries before. After all these preliminaries, Elsasser finally articulated a clear point of departure for his own scientific journey, which justifies continued interest in his work: “Close reasoning indicates the existence of an alternative to reductionism. This is so despite the fact that the laws of quantum mechanics are never violated.”
From this point on, we have quite an exciting journey ahead of us. Indeed, biology is a “non-Cartesian science.” The “master concept” in describing the holistic properties of the living is complexity (p. 3), more precisely, what he describes as unfathomable complexity. This concept dominates the entire endeavor; therefore an extended quotation is probably justified. Unfathomable complexity

“implies that there is no series of actual experiments, and not even a set of suitably realistic thought—experiments such that it would be possible to demonstrate the way which all the properties of an organism?can be reduced to consequences of molecular structure and dynamics?.”

Furthermore, he defines as morphological properties those that remain unaccounted for by physics and chemistry. Four principles and a “basic assumption” stand at the foundation of his biology. The assumption refers to the holistic view adopted—the living cannot be understood and described other than as a whole: “the organism is a source (or sometimes a sink) of causal chains which cannot be traced beyond a terminal point;” that is, they are ultimately expressed in the unfathomable complexity of the organism.
According to this viewpoint, extreme events in the living cannot be meaningfully addressed on the basis of reductionism (not even at the level of detail of single neuron functions or genetic expression), but only globally, in a holistic manner.
The first principle that Elsasser further articulates is known as ordered heterogeneity. It states that, as opposed to the homogenous nature of physical and chemical entities (all electrons are the same), the living consists of structurally different cells. There is order at the cellular level, and heterogeneity at the molecular level. Heterogeneity corresponds to individuality, a term that has no meaning in the physical world. The principle of creative selection is focused on the richness of living forms. For homogenous systems, the variation of structure (if there is such a variation) averages out. For heterogenous systems, i.e., the living, an immense multitude of possible states is open to realization, i.e., selection. The property of selection is attributed to matter alone—a more refined mathematics of dynamic systems, which to date has not been formulated would here probably define some specific self-organizing action. The selection as such is based on the third principle, of holistic memory. The new morphological pattern actually selected resembles earlier patterns, but is not the realization of stored information. Elsasser is quite convincing in arguing for a “memory without storage”—the touchstone of the theoretical scheme proposed” (p. 43). The argument is based on the distinction between two processes: homogenous replication—the assembly of identical DNA molecules—and heterogenous reproduction—a self-generation of similar though distinct forms.
Always different, the living practices creativity as a modus vivendi. Replication is a “dynamic process” (p. 75) resulting in what we perceive as regularities in the realm of the living. Replication and reproduction need to be conceived together. What makes this possible is the fourth principle, of operative symbolism. The discrete, genetic message is represented by a symbol that stands for the integrated reproductive process. Elsasser himself realized that this operative symbolism is merely a tag for all processes through which the living experiences its own dynamics. He looked for a triggering element, a releaser, as he called it, that could start a restructuring process. From a piece of genetic code, the releaser will trigger the generation of the complete message necessary for the reconstruction of a new organism. We can imagine this releaser—the operative symbol—as able to start a “program” that will result in a new biological form, as an alternative to storing and transmitting the form itself. The biological information is stored as data (in the homogenous replication) and as a space of an immense number of alternate states from which one will eventually be realized (in the heterogeneous reproduction). This later assumption implies that biological phenomena are “in part” autonomous.
Again, for the study of extreme events in the living—to which not only epileptic seizures and strokes belong, but also cancer and heart attacks—these observations are a good guide for prevention and anticipation. That earthquakes and hurricanes are always different, as are strokes and financial market crashes, speaks for the adoption of the over-arching notion of heterogenous replication.
Instead of searching for laws, Elsasser highlights regularities. Where reductionists would expect that “the gametes contain all the information required to build a new adult,” a non-reductionist biology would rely on holistic memory and his Rule of repetition: “Holistic information transfer involves…the reproduction of states or processes that have existed previously in the individual or species as the case may be” (p. 119). Of special interest to him is the re-evaluation of the meaning of the Second Law of Thermodynamics (and the associated Shannon law of information loss). Elsasser argued that since paleontology produced data proving the stability of the species (over their many millions of years of existence), and since the Second Law of Thermodynamics points in the opposite direction, only a different integration of both these perspectives can allow us to understand the nature of the living. Therefore, two types of order were introduced, in a way such that they never contradict each other. This is what he called biological duality: “living things can be described by a different theory as compared to inanimate ones.” As a consequence, if one attempted to verify holistic properties, a different kind of experiment from the one conventionally used in physics would be required. It is worth mentioning here that Wilhelm Windelband [33] made the distinction between nomothetic and idiographic sciences, the latter focused on singularity: “der Gegensatz des Immergleichen und des Einmaligen,” (the contradiction of the invariable/unchanging and the unique).
It is at this juncture that Rosen’s thinking and Elsasser’s meet—I doubt that they had a chance to study in depth each other’s work on the living and life. Rosen was “entirely dedicated to the idea that modeling is the essence of science” [34]; Elsasser realized that no experiment, in the sense of experiments in physics, could capture the holistic nature of the living. Moreover, both asked the fundamental question: What does it take to make an organism? If the representamen R for an organism (such as the stem cell) were available, we would be able to anticipate extreme events in the living in relation to the end of life (return to physicality). But extreme events can also be viewed from the perspective of the same question: What does it take to make an earthquake? Or an act of terrorism? Elsasser, not unlike Rosen, concluded: “The synthesis of life in vitro encounters insuperable difficulties” (p. 155). It is quite possible that such a strong statement corresponds to the realization that anticipation, as the final characteristic of the living, might be very difficult to describe—the analytic step—but probably impossible to reproduce—the synthesis. So, we might even be able to say what it takes to create a certain extreme event, but that does not mean that we could literally make it. Even induced seizures are not exactly like the ones experienced by individuals who go through real seizures. Low-scale earthquakes (caused by experiments and tests that researchers conduct) are not by their nature of a different scale and quality than the ones that people experience on the Islands of Japan, in California, in China, or in Turkey. It is therefore of particular interest to take a closer look at the various factors involved in what, from a holistic perspective, appears to us as anticipatory.
We learn from this that there is no anticipation in the realm of physics. Accordingly, if we are dedicated to addressing extreme events—whether in the physical world or in the realm of the living (birth and death are themselves extreme events)—we need to realize that answers to what preoccupies us will result from understanding how the living anticipates. (We know why, since this results from the dynamics of evolution.)
The final thesis of this article is of less significance to prediction of extreme events and more to our anticipatory condition in the universe. Fifth thesis: The project of extreme scientific ambition of creating life from the physical can succeed only to the extent that a physical substratum can be endowed with anticipatory characteristics.
This conclusion is not a conjecture; it is strongly related to our better understanding of extreme events. It ascertains that in addressing questions pertinent to extreme events, we are bound to address, differently than Rosen did, the notion of what life is. After all, nothing is extreme and nothing is an event unless it pertains to life.
References and Notes
1. Heraclitus, as mentioned in Plato’s Cratylus, 402a.
2. “Indeed, representation necessarily involves a genuine triad. For it involves a sign, or representamen, of some kind, inward or outward, mediating between an object and an interpreting thought. . . .” The Logic of Mathematics (1896). In: Collected Papers: 1-480
3a. Peirce, Charles Sanders: Peirce, Charles Sanders. “A sign is something which stands for another thing to a mind.” Of logic as a study of signs, MS 380 (1873)
3b. “Anything which determines something else (its interpretant) to refer to an object to which itself refers (its object) in the same way, the interpretant becoming in turn a sign, and so on ad infinitum” (1902). In: Collected Papers: 2.303
3c. “A sign is intended to correspond to a real thing.” Foundations of Mathematics, MS 9 (1903)
4. Schneiderman, Ben: Designing the User Interface. Addison Wesley, Boston (1998)
5. Morris, Charles: Foundations of the Theory of Signs. In: International Encyclopedia of Unified Science (Otto Neurath, Ed.) vol. 1 no. 2. University of Chicago Press, Chicago (1938)
6. Nadin, Mihai: Zeichen und Wert. Gunter Narr Verlag, Tü bingen (1981)
7. Marty, Robert. “Catégories et foncteurs en sémiotique,” Semiotica 6. Agis Verlag, Baden-Baden (1977) 5-15
8. Marty, Robert. “Une formalisation de la sémiotique de C.S. Peirce à l’aide de la théorie de categories,” Ars Semeiotica, vol. II, no. 3. Amsterdam: John Benjamins BV (1977) 275-294
9. Marty, Robert. L’algebre des signes. Amsterdam/Philadelphia: John Benjamins (1990)
10. Goguen, Joseph: Algebraic Semiotic Homepage http://www.cs.ucsd.edu/users/goguen/projs/semio.html
11. Extreme Events: Developing a Research Agenda for the 21st Century, sponsored by the National Science Foundation, organized by the Center for Science, Policy, and Outcomes (CSPO) at Columbia University; and the Environmental and Societal Impacts Group of the National Center for Atmospheric Research, Boulder. Colorado, June 7-9, (2000)
12. Gallese, Vittorio: The Inner Sense of Action. Agency and Motor Representation. In: Journal of Consciousness Studies 7, no. 10, (2000) 23-40
13. Nadin, Mihai: The Civilization of Illiteracy. Dresden University Press, Dresden (1997)
14. Gödel, Kurt: Über formal unentscheidbare sätze der Principia mathematica und verwandter systeme. In: Monatshefte fü r Mathematik und Physik, 38 (1931) 173-198; translated in van Heijenoort, From Frege to Gödel, Cambridge:Harvard University Press, Cambridge (1971). The exact wording of his first theorem is “In any consistent formalization of mathematics that is sufficiently strong to define the concept of natural numbers, one can construct a statement that can be neither proved nor disproved within the system.” His second theorem states: “No consistent system can be used to prove its own consistency.”
15. Rosen, Robert: Anticipatory Systems. Pergamon Press, New York (1985)
16. Nadin, Mihai: Anticipation: The End Is Where We Start From. Lars Mü ller Verlag, Basel (2003)
17. Rosen, Robert: Life Itself: A Comprehensive Inquiry into the Nature, Origin, and Fabrication of Life. Columbia University Press, New York (1991)
18. Berry, II, Michael J., I.H. Brivanlou, T.A. Jordan, M. Meister. Anticipation of moving stimuli by the retina. In:.Nature 398 (1999 ) 334-338
19. Ekman, P., W.V. Friesen: Facial action coding system: A technique for the measurement of facial movement. In: Consulting Psychologists Press, Palo Alto (1978)
20. Fletcher, P.C., J.M. Anderson, D.R. Shanks, R. Honey, T.A. Carpenter, T. Donovan, N. Papdakis, E.T. Bullmore: Responses of human frontal cortex to surprising events are predicted by formal associative learning theory. In: Nature Neurosciences, 4:10 (October, 2001) 1043-1048
21. Ishida, Fumiko, Yasuji F. Sawada: Human Hand Moves Proactively to the External stimulus: An Evolutional Strategy for Minimizing Transient Error. In: Physical Review Letters, vol. 93, no.16, Oct. 15 (2004)
22. Nadin, Mihai: Mind—Anticipation and Chaos. Belser Verlag, Stü ttgart/Zü rich (1991)
23. Minsky, Marvin: The Virtual Duck and the Endangered Nightingale. In: Digital Media,
June 5 (1995) 68-74
24. Nicolis, Miguel, A.L., Dragan Dimitrov, Jose M. Carmena, Roy Christ, Gary Lehew, Jerald D. Kralik, Steven P. Wise: Chronic, multisite, multielectrode recordings in macaque monkeys. In: Proceedings of the National Academy of Sciences of the Unites States of America, PNAS Online, Sept. 5 (2003)
25. Quoetone, Elizabeth, Keneth L. Huckabee: Anatomy of an Effective Warning: Event Anticipation, Data Integration, Feature Recognition. In: www.wdtb.noaa.gov/resources/ PAPERS/sls00/slsPaper/page4.htm (1995)
26. Guiasu, Silvio: Comment on a paper on possibilistic entropies. In: International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 10, no. 6 (2002) 655-657
27. Feynman, Richard: Potentialities and Limitations of Computing Machines, lecture series, California Institute of Technology (1983-1986)
28. Feigenbaum, Mitchell: Universal Behavior in Non-linear Systems. In: Los Alamos Science, 1 (1980) 4-27
29. The Scientific Rationale of the British Ecological Society (BES) Symposium, March-April 2005. See symposium announcement at www.britishecologicalsociety.org/articles/meetings/current
30. Montgomery, Richard: Nonholonomic Control and Gauge Theory. In: Nonholonomic Motion Planning (J. Canny and Z. Li, Eds.). Kluwer Academic Press (1993) 343-378
31. Heisenberg, Werner: Uncertainty Principle, first published in Zeitschrift fü r Physik, 43 (1927) 172-198
32. Elsasser, Walter M.: Reflections on a Theory of Organisms. Johns Hopkins University Press, Baltimore. Originally published as Reflections on a Theory of Organisms. Hoilism in Biology. Orbis Publishing, Frelighsburg, Quebec (1987)
33. Windelband, Wilhelm: Geschichte und Naturwissenschaft (1894)
34. Rosen, Robert: Essays on Life Itself. Complexity in Ecological Systems. Columbia University Press, New York (2000) 324