The anticipatory profile. An attempt to describe anticipation as process
Special issue dedicated to anticipation (edited by Mihai Nadin) of International Journal of General Systems, Vol. 41, Issue 1, 2012, pp. 43-75. PDF Inductive class representation and the more comprehensive evolving transformation system (ETS) are congenial to the subject matter of anticipation. In substantiating this assertion, we examine the epistemological premises of a new form […]
Special issue dedicated to anticipation (edited by Mihai Nadin) of International Journal of General Systems, Vol. 41, Issue 1, 2012, pp. 43-75.
PDF
Inductive class representation and the more comprehensive evolving transformation system (ETS) are congenial to the subject matter of anticipation. In substantiating this assertion, we examine the epistemological premises of a new form of representation, of interest to pattern recognition and Artificial Intelligence (AI), but even more to the study of living systems. Some concepts, such as classes, time and time scale, and generative processes are examined in detail with respect to their pertinence to anticipation. Finally, pattern generation and ETS programming are suggested.
Now when we get to the inductive stage what we are about is finding out how much like the truth our hypothesis is, that is, what proportion of its anticipations will be verified. (C.S. Peirce 1905)
1. Introduction
The question of whether real-life phenomena – ranging from those that fit deterministic descriptions to more complex developments – can be specified in some systematic manner becomes more critical as the state of available knowledge elicits more daring scientific concepts, such as those advanced in genetic medicine, nanotechnology, bioengineering, and quantum computation, to name just a few. The expectation of uniform expression of knowledge has never been higher, although the variety of forms through which knowledge is acquired and disseminated is increasing very fast. These epistemological themes are unavoidable, especially in pursuing research work at the confluence of several disciplines. As much as specialization has contributed to our understanding of the world, the major challenge in our days is no longer to explore the centre (of a particular discipline), but the vast area of shared interest among many specializations. Accordingly, scientists cannot escape asking questions formerly relegated to philosophers, and somehow understood as having only philosophical significance. ‘How is knowledge represented across disciplines?’ is such a question.
2. Structural measurement and self-organization
In search of productive hypotheses transcending the current state of the mathematical foundation, scientists seek alternatives. Some can be found in work carried out in the past; others in work in progress originating from researchers whose work has not yet been fully acknowledged. I entered dialogue with many distinguished researchers known to venture into the inter- and trans-disciplinary: the late Herbert Simon, Eric Kandel, Solomon Marcus, Lotfi Zadeh, Daniel Wolpert, George Klir, and Joseph Goguen, among others. In 2002, Jeffrey Nickerson drew my attention to Lev Goldfarb’s work. Now a professor at the Stevens Institute of Technology, Nickerson has dedicated a great amount of interest to issues of representation. (He received a BA from UC, Berkeley, went on to do graduate work in graphic design at the Rhode Island School of Design, and in 1994 received his Ph.D. in Computer Science from New York University.) And so, unbeknownst to Goldfarb and his occasional co-authors – let me mention Golubitsky, Korkin, and Gay – I myself became, for a while, a student of what Goldfarb calls the evolving transformation system (ETS). Consequently, I came to realize that some of the questions – regarding representation and quantification, in particular – arising from my research in anticipatory systems were to some degree addressed within the representation Goldfarb proposes.
At the origin of interest in a different mathematics to be considered in relation to the subject of anticipation this contribution to the significance of Goldfarb’s system is the following text that describes the framework of Seneludens, a multi-year research project focused on anticipation and ageing:
The congenial perspective of the integrated structure of the information processing underlying anticipatory processes is that of structural measurement process (SMP). The biologically inspired ETS formalism is the mathematical foundation for a structural measurement process (Goldfarb et al. 2000). ETS is a dynamic record of the interaction of elements involved in the functioning of a system, better yet in its self-organization. The inductive learning process is represented in the record of the experiment through which anticipatory characteristics are captured. Each time we are involved in a specific action, learning takes place. The premise is straightforward: Anticipation is always expressed in action (Nadin 2007). The experimental setting, called AnticipationScope® , considers various motoric, physiological, cognitive, sensorial, and perceptive processes integrated in real-time anticipation. The perspective is ‘congenial’ because, as we shall see, the description of action and the realistic animation that describes the action by cinematographic means constitute a structural measurement process (see SMP above). Actions embodied in an artificial animated character are highly correlated.
Motion capture is the means for describing in detail the performance of certain actions (part of an experiment). The AnticipationScope integrates high-resolution motion capture as a scientific platform for producing reactive animations. Reactive animations (Efroni et al. 2005) serve as an interface between the knowledge domain represented (in our case, the human being’s sensory, cognitive, and motoric characteristics) and the new applications to which the knowledge domain relates: exploration of means and methods for stimulating brain plasticity. Interactive games are among such means. We intend to eventually use such reactive animations in wearable computers designed to assist persons with anticipatory deficits (the elderly, in particular). The integration of number-based descriptions and qualitative procedural descriptions (e.g. balance and postural dynamics, collision avoidance, timing of tool use, etc.) allow for the desired structural measurement process, which further qualifies the originality of the research. The goal is not to replicate the routine musculo-skeletal description of biomechanics, performed in many excellent laboratories, but to reach a new level of subject-in-action description. Electromyography (EMG), electrodermal activity (EDA), electrocardiogram (EKG), and other parameters (such as applied force by hand and foot, tympanic temperature, salivary hormones, blood pressure, pulse oximeter, skin temperature, goniometer, accelerometer, spirometer, galvanic skin response meter, somatosensory evoked potentials, infrared eye tracking system, acquired through a variety of sensors) generate corresponding data streams. These data streams, each with its own time scale, modulate the high-resolution descriptions acquired in the matrix format motion capture environment.
(For a detailed description, see http://www.anteinstitute.org/index.php?page=seneludens.)
To capture dynamics, researchers have defined the expectations of experiments, quantification methods, and interpretation guidelines. As we shall see, anticipation, as a dynamic characteristic, requires that action be captured holistically, not just as particular instances of an action, which is the usual case. It requires that the experiments engage each individual as a complex whole in order to avoid concentration on a particular part of the body. Above all, the measurement process must be structural, that is, it should not produce only numbers, as quantitative descriptions of the processes observed, but also descriptions of integrated operations, in particular, the class transformation system: how a certain movement becomes part of another ensuing movement, i.e. action. Without the ETS, which simultaneously captures the qualitative and quantitative characteristics of processes, this task is currently not within our reach (Nadin 2005). The research proposal submitted to the National Science Foundation was positively evaluated by some, but caused other reviewers to consult dictionaries and to ‘Google’ more than they usually do. Their education did not involve the notion of anticipation as a subject of scientific interest. No alternative to the reductionist-deterministic understanding of causality – advanced by Descartes, and pursued since his time as the exclusive matrix of rationality – ever percolated in their representation of reality. This epistemological discontinuity is similar to that experienced by physicists who grew up before quantum mechanics, or of biologists who were educated before what we have learned about DNA. The phenomenon is beyond the scientific comprehension of those locked in the prejudices resulting from the generalization of incomplete knowledge. The situation will not be different should they examine a mathematical system that challenges none other than the sacrosanct number- based measurement mechanism prevalent in today’s world of experiments.
2.1 Anticipatory systems
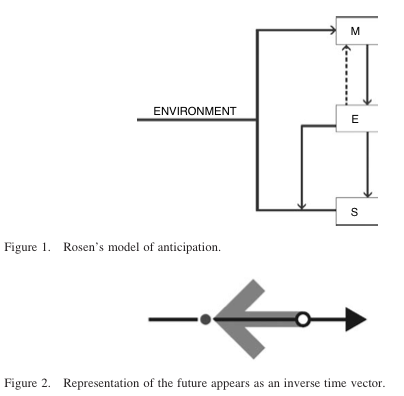
The following operational definition of an anticipatory system is submitted for the sake of clarity and brevity: ‘An anticipatory system is a system containing a predictive model of itself and/or of its environment that allows it to change state at an instant in accord with the model’s predictions pertaining to a later state.’ (Rosen 1985, p. 339)
Rosen distinguished the difference between the dynamics of the coupled given object system S and the model M. That is, the difference between real time in S and the modelling time of M (faster than that of S) is indicative of anticipation. Albeit, time in this particular description ceases to be an objective dimension of the world, since we can produce quite a variety of related and unrelated time sequences. He also remarked that the requirement of M to be a perfect model is almost never fulfilled. Therefore, the behaviour of such a coupled system can only be qualified as quasi-anticipatory (E represents effectors, through which action is triggered by M within S). Rosen named, rather ambiguously, as aspects of this functioning: planning, management, and policies. Essential here are the parametrization of M and S, and the choice of the model. The standard definition, quoted again and again, is not only contradictory – as Dubois (1996) noticed – but also circular – anticipation as a result of a weaker form of anticipation (prediction) exercised through a model.
Much more interesting are Rosen’s (1991) examples: ‘If I am walking in the woods and I see a bear appear on the path ahead of me, I will immediately tend to vacate the premises;’ the ‘wired-in’ winterizing behaviour of deciduous trees; the biosynthetic pathway of cells with forward activation. These patterns result from inductive learning (small sample, also known as case study); and to a certain degree, we not only recognize these patterns, but we can also express them in some formal way. Each of these examples sheds light on the distinction between processes that seem vaguely correlated: background information (what could happen if the encounter with the bear took place, based on what has already happened to others); the cycle of day and night and the related pattern of lower temperatures as days get shorter with the onset of autumn; the pathway for the forward activation and the viability of the cell itself. What is not at all clear is how less-than- obvious weak correlations end up as powerful anticipation links: heading away from the bear (‘I change my present course of action, in accordance with my model’s prediction.’ Rosen 1985, p. 7) usually eliminates the danger; loss of leaves saves the tree from freezing; forward activation, as an adaptive process, increases the viability of the cell. We have a ‘temporal spanning’, as Rosen called it, or as Goldfarb would call it, a formative path. In Rosen’s example of senescence (‘an almost ubiquitous property of organisms’, ‘a generalized maladaptation without any localizable failure in specific subsystems’, (Rosen 1985, p. 402), it becomes even more clear that the time factor is of essence in the biological realm. Indeed, as I have shown (Nadin 2003, p. 101), the future is an informational future.
The model unfolds in faster than real time, and as it affects the state of the system, it appears as a future in relation to the real-time unfolding of events.
When Dubois (and others) tried to formalize Rosen’s definition:
![]()
they ran into a problem. In this expression, x is the state variable of the system, t stands for time (present, t–1 is the past, t þ 1 is the future), and p is a control parameter. Dubois (1996) starts from recursion within dynamical discrete systems, where the future state of a system depends exclusively on its present and past:
![]()
He further defines incursion, i.e. an inclusive or implicit recursion, as:
![]()
and exemplifies its simplest case as a self-referential system. The embedded nature of such a system (it contains a model of itself) explains some of its characteristics, in particular the fact that it is purpose (i.e. finality, or telos) driven. Structural dynamics, which the mathematics of dynamic systems defines through attractors, often appears as having a similar condition.
In Rosen’s view, since the ‘heart of recursion is the conversion of the present to the future’, (Rosen 1991, p. 78), and anticipation is an arrow pointing in the opposite direction, recursions could not capture the nature of anticipatory processes. Incursion (as inclusive incursion) and hyperincursion (an incursion with multiple solutions) describe a particular kind of predictive behaviour (Dubois 1996). However, the best we can expect from such descriptions is a model of anticipation – eventually, a computational model – but not an effective representation of anticipation itself.
Based on a variety of arguments similar to what was just spelled out, an alternative definition of an anticipatory system can be advanced: an anticipatory system is a system whose current state depends not only on previous states, but also on possible future states (Nadin 2003, p. 53). (For more on anticipation, check out the website, www.anteinstitute.org, the anticipation knowledge portal, www.anticipation.info, and Nadin 1991, 2003).
2.2 Modelling the living
Physical models (such as wind tunnels), statistical models, or numerical models might help researchers capture some aspects of anticipation, but only to the extent to which they limit themselves to generalizations based on previous events and accept a probability- based form of anticipation, i.e. prediction. The thesis advanced in this text is that, in anticipation processes, we cannot avoid the expression of physicality. Nevertheless, we have to go beyond it by capturing the expression of characteristics specific only to the living. In the physics domain, there is a clear expression of invariance in space and time; in the living, this is not the case. As is known, process models are always incomplete estimates of how the real world functions. The degree of incompleteness in the realm of the living is higher by far than what is reached in physics or chemistry. Accordingly, explanatory models are the best we can expect in using the modelling so far mentioned. Statistical predictive models, numerical models (with all the initial observed data and parametrization aspects), and all other process models remain inadequate for the knowledge domain of anticipation, which is the epitome of interactive complexity. Once again, this makes the perspective of evolving systems so attractive.
Since we shall return to the subject, let us only mention here that the fundamental problem with statistical or numeric descriptions, even with process models, is that of a mathematical foundation that cannot escape its Cartesian reductionist premise. With respect to anticipation, one cannot fraction the process – as the Cartesian method suggests – without actually slipping from an anticipatory pattern into a reactive pattern. If we engage in discrete descriptions, we actually fracture the whole, and end up focusing on parts. This might be scientifically interesting, but not relevant to the intricate complex to which the parts belong. The structure dissolves; what remains are the elements that constituted a structured togetherness, but that now claim their own relevance, in contrast to the complexity of the whole of which they are only a part.
Robert Rosen, the mathematician of the end-of-the-last-century’s biology, tried to avoid this pitfall by adopting category theory as a formalism for describing anticipation. In Rosen’s category theory description, entailment expresses relations among the elements of a system. The emphasis here is on the relational perspective. And one can only admire the elegance of the representation adopted for encoding natural systems into formal systems. However, all known limitations of category theory, in particular, the way time is considered, speak in favour of looking for some other representational mechanisms. Before discovering structural measurement, I focused on C.S. Peirce’s diagrams. But once I read What is a Structural Measurement Process? (Goldfarb and Golubitsky 2001), I realized that this was an alternative to an almost impossible situation: we are aware of anticipation in the real world of the living, but our current descriptions seem to indicate that anticipation is either impossible or, whenever we experience it, it should be, against the experimental evidence, reducible to control mechanisms or to probability-based descriptions (including the fashionable Bayesian formula). Natural sciences, experiencing a formidable revival in our days, screamed for a mathematics appropriate to their condition. ETS might be a good candidate.
2.2.1 The possible
In the realm of physics, probabilities appropriately help in inferring from experiences of the past to the future. In the realm of the living, probabilities are only of limited relevance (Figures 1 and 2). Take a simple example (cf. Figure 3): a stone repeatedly dropped from the same height will always fall in ways that we can describe with a high degree of
precision (using physics theory and the mathematical representation associated with it). If we let a cat fall from the same position, it will never fall the same way twice. The stone remains the same, for all practical purposes. The cat changes: ageing, learning, new context. The probability-based model is helpful in many instances – from descriptions of weather patterns to constructing machines and bridges – but not for describing how the cat will eventually fall.
The current mathematics of such description (cf. Figure 3, the bottom of the image) is based on applied differential geometry (Montgomery 1993). This allows for an approximate description of an object flipping itself right side up, even though its angular momentum is zero. The movement of paws and tail conserves the zero angular momentum. The final upright state (if the anticipation does not fail) has the same value. The geometric phase effect, or monodromy (no angular momentum), is accurate, provided that no interactions take place. However, in observing the falling cat, we are not passive entities (even if we do not intervene at all), but co-producers of the event. The only pattern we can infer is that of preserving the coherence of the process. If an accident happens, the event appears to us as incoherent. The pattern recognition (PR) implicit in the differential geometry description is accurate to the extent that it can be integrated in AI procedures. (Montgomery even mentioned that he described the falling of a robot.) As we know, such procedures are relevant to what we define as an expert domain. In the living, in addition to acknowledging the physicality of the entity – a cat is made out of matter – we have to acknowledge a specific non-repetitive dynamics that affects learning. Stem cells are made of substances we know how to identify and measure at almost any instance in time. Although fundamentally the same, no two stem cells will unfold into identical human beings. The probability description is ultimately irrelevant to the unfolding of stem cells ( Figures 4 and 5).

What emerges in an even summary examination of such phenomena is the need to consider a correlate of probability; and this, so far, is possibility. Possibility distribution excludes the existent (what is), but opens the door to what will not duplicate any extant entity. Details on possibility theory (triggered by Zadeh’s 1978 seminal Fuzzy Sets as the Basis for a Theory of Possibility) would be out of place here. Suffice it to say that it

provides means for modelling imprecision and uncertainty (not just in language representations). The creative unfolding of stem cells is yet another expression of anticipatory processes, making clear that the process involves the probable and the possible, understood in their very elaborate interrelationship that involves the attractor of necessity. In view of the fact that possibilities are qualitative descriptions, which at most are expressed in such evaluations as those inspired by Zadeh’s fuzzy set theory, it follows that the mathematics we need in order to capture anticipation ought to accommodate quantity- and quality-based representations. This mathematics also has to reflect the relational nature of the structural dynamics of such systems.
With this rather sketchy awareness of what anticipation is about, it should become clear that all known representations based on numbers can only partially capture aspects of the rather complex behaviour that results from deterministic and non-deterministic processes. Moreover, anticipation is acquired through those formative processes we call learning. The small set of information associated with meaning (Davies 2004) that partakes in the learning process exemplifies inductive learning. Last but not least, anticipation is expressed in the adaptive performance that underlies every form of evolution.
2.3 What is there to measure? What is there to represent?
Let us provide some additional examples that will not only shed more light on what is meant by anticipation, but also on the high requirements for an adequate representation of what is involved in an anticipatory process. The reason for this exercise is twofold: first, to see what kind of measurements (if any) we might need to conceive for capturing knowledge about anticipation; second, to shed light on the PR dimension of anticipation.
Change in posture – standing up from a seated position, for example – would cause changes in blood pressure. This is the ‘physics’ of the body: a liquid (blood, among others), pipes (the various blood vessels and other conduits), a pump (the heart), a control mechanism (associated with the brain). This image, rooted in the rationality of ‘the human being as machine’, (Descartes, Discours de la methode 1637; La Mettrie, L’homme machine, 1748; see Thomson 1996) is a good starting point. A rubber tube with liquid inside can serve as a functional model for explaining the mechanism.
The pressure of the fluid in the rubber tube varies as we change its position from horizontal to vertical. If human beings were subjected to blood pressure variations as often as they change posture, they would have a terrible time. Dizziness is only one of the symptoms accompanying variations in blood pressure. It appears that a certain reflex, called the baroreceptor reflex (Kirchheim 1976, p. 107) – some even call it the anticipatory reflex – affects the heart rate via the nervous system in order to maintain the blood pressure within relatively constant and safe limits. How does the heart ‘know’ about a change in position? Obviously, the analogy to the simple physical system of a machine, with liquid, pipes, and pump works only in a limited way. The stone we drop does not know and cannot actively affect the way it falls; the cat affects its falling. The question asked – ‘How does the heart, or whatever controls the heart, know what the body will do?’ – goes beyond the physics of pumping a liquid through pipes. Here is where the specific domain of anticipation starts, and where ETS becomes relevant to its study. We recognize an overarching pattern – maintain blood pressure constant – and we recognize what contributes to it. But we still do not know how to represent the many factors leading to the pattern, i.e. how to produce a structural representation of the dynamics specific to this subsystem of the human being.
Anticipation is a characteristic of the living, but not a specific action or activity. We do not undertake anticipation. It is not a specific task, and it appears to us as autonomous. Anticipation is the result of a variety of processes. We are in anticipation. As an outcome, anticipation is expressed through consequences: increased performance (an anticipated powerful tennis serve is successfully returned); danger (such as a passing car that a short time ago was not within our sight) is avoided; an opportunity (in the stock market, for instance) is used to advantage. Anticipatory processes, implicit in the functioning of the living, result in the proactive dimension of life. Anticipatory processes are defined in contrast to reactive processes. Characteristic of the deterministic sequence of action– reaction defined in physics, reaction is the expression of our physical nature.
No matter what individuals do, the doing itself – to which explicit and implicit learning belongs – is what defines their unfolding identity. The outcome is the expression of physical and intellectual abilities. The return of a very fast tennis serve is never only a matter of reaction. The PR component – learning supports the identification of patterns of serving – is far from trivial. In competitive situations, anticipations define all the individuals involved in the interaction: the serving player, the receiving player, and the entire context of the tennis game, including the referees. After the experience, a variety of cues can be interpreted as leading to the PR. Others, no less significant, lead to signalling different patterns. To represent such processes means to preserve their holistic unity, to avoid fractioning that which ends up being a whole: the successful serve or the successful return. To simply associate success to numeric values, such as the ball’s speed and spin, racquet characteristics, etc., is useful for obtaining details, but not for reconstructing the correlations behind the anticipation expressed. Unlike tennis, chess turns out to be primarily an expression of anticipation that engages intellectual abilities, although, in some defining ways, the physical is also engaged. Playing with a chess program is different from playing with another person.
Anticipation, regardless of the specific domain in which it is at work, reflects knowledge and experience. Some would argue that the knowledge in question is PR, and the experience is that of learning. Expression of goals, whether they are specifically spelled out or implicitly assumed, affects the outcome of human actions as well. The process through which existence is preserved at the lowest level – like the phototropic mono-cell – exemplifies the idea. The higher complexity living – the human being, for example – is equally characterized by finality (purpose). At a certain level of life organization and complexity, the preservation drive takes new forms through which it is realized. Anticipation is the common denominator. However, the concrete aspect of how anticipation is eventually expressed – i.e. through self-awareness, intentionality, or in the activity we call ‘planning’ – changes as the complexity of the processes through which the living unfolds increase. To represent such changes, fundamentally different from the change in weather, or the change affecting a falling or stationary stone, we need means that encode both qualitative and quantitative aspects of reality, as this is subject to dynamics (its own and the dynamics of interaction). In other words, we need to effectively account for process as an expression of formative dynamics. Machine PR and machine learning will make progress as knowledge derived from formative dynamics is captured in computational form; or as we advance new computational means, transcending the limitations of determinism.
3. Dynamics and representation
To the best of our knowledge, Goldfarb did not specifically have in mind phenomena like those described above. When Goldfarb (2006b) describes a person sitting on a chair, he leaves out the anticipatory process guiding the sitting itself. Without anticipation, a person who sits down would be subject to the physics of action (weight falls on the seat) and reaction (equal force applied to the buttocks – that can hurt! – recall Newton’s third law of motion). Moreover, Goldfarb specifically does not accept the clear-cut distinction between the physical and the living that we advance. He operates in the continuum of reality as it is subject to change. I came to know his views as we engaged in a dialogue occasioned by his lecture at the Massachusetts Institute of Technology (Goldfarb 2006a). We met and argued some fine points of his broad concept of representation. And we agreed that the final proof of his assertions will be the scientific developments that they will prompt. Several projects of common interest (concerning ETS and anticipation, of course, but also ETS and risk assessment, or ETS and design) were carried out (Nadin 2009). But on this note, it becomes clear that the different perspective of science that Goldfarb proposes begs questioning its premises, assumptions, methods, and relevance.
Before I writing the text for the Seneludens research proposal that identified the structural measurement process as congenial to anticipatory processes, we had to evaluate ETS in its entirety, not only as a technical convenience that could substitute for the number-based perspective. The ETS derived from representational formalism comes to expression in contradistinction to generalized number-based knowledge representation. Over 20 years of never-ending refinements resulted in a plethora of articles that make sense in the context of the system proposed. (Goldfarb is currently working on a book about his mathematics.)
Goldfarb does not seek the complexity ‘alibi’ as he carries out his work. In general, he does not fall prey either to the politics of science (expressed in its ever-changing slogans) or to the pitfalls of scientific opportunism (that is, the concepts in fashion that translate into NSF, NIH, or NEH grants). He actually dares to carry out fundamental research in a day and age of ever-shorter cycles of scientific focus, driven by promising, but short-lived, applications. He has an explicit programme: how to capture and express change of all objects in the universe. This does not exclude the possible revelation that not all objects in the universe change the same way. He defines an epistemological foundation that puts the notion of class in its focus. The presentation entitled The first class(ification)-oriented representational formalism, to which reference was made above (Goldfarb 2006b), bears the provocative subtitle: Do you know what a class is? We shall return to this question to, since all of us should take this interrogation as more than rhetorical. The class-generating system outputs not only entities belonging to the class, but also their formative histories. Thus the emphasis is on learning, more precisely on inductive learning processes. To bear knowledge about change means to go beyond the distinction between an initial state (chosen as a reference) and a (provisional) final state. A representation of change has to be powerful enough to address the variety of elements conducive to change.
Since semiotics (in Peirce’s broad view) has played a defining role in my own formative path, I am sensitive to everyone in search of new means of representation. But I am allergic to all those who speak about representation without understanding what it is. Let us be clear: this is not his case. In terms no different from Goldfarb’s in deploring the fact that AI failed to recognize PR’s specific contribution, and thus performed well below everyone’s expectations, I deplored the fact that AI ignored semiotics in attempting to describe what intelligence is and how we can emulate it in silicon. But this aside should not preclude our attempt to get to the core of what Goldfarb (along with his collaborators, all to be acknowledged for embracing his ideas) broadcasts as a new form of representation.
3.1 ETS in context
If one could define a class of those scientists who have focused on representation, Leibniz, Peirce, as well as Robert Rosen and Goldfarb himself would belong to it. The attempt to address representation is scientifically challenging, but not rewarding. Representation is a fundamental dimension of all science; but rarely, if at all, has anyone’s focus on representation proved beneficial for the person’s scientific reputation. Neither Leibniz nor Peirce, in their time, even less Rosen, more recently, were properly acknowledged. This is an old story. We take our representations – the symbolism of mathematics, chemistry, logic, etc. – for granted, never questioning the influence of representations adopted on what we do, and how we communicate what we learn in the process of doing.
3.1.1 Leibniz and representation. Why representation is important
The history of science mentions the conflict between Newton and Leibniz, without properly showing how their different representations – they used a different formalism for defining calculus – actually lead to different sciences. That Leibniz invented a language of 0s and 1s – the lingua adamica (described in Nadin 1997) – is seen almost as a historic quirk, not as a foundational step. In his New Year’s letter (2 January 1697) to the Herzog (Duke) Rudolph August, Leibniz brought to fruition work started 20 years earlier (De progressione dyadica is dated 17 March 1679) on binary representation. (His teacher, Erhard Weigel, influenced by Pythagoras, had tried his hand at expressing moral wisdom in arithmetic language.) With this representation, exemplified in a Gedenkmü nze (memorial coin) celebrating the accomplishments of his benefactor, Leibniz went as far as to provide a synthetic image of his accomplishments, with everything expressed in 0s and 1s. But this was only a beginning. In his attempts to deal with Chinese philosophy, he used a different dyadic representation, a line and a broken line, in order to report on the philosophy of Fuh-Hi, in particular the book I-Ching (Book of Changes). While seeking a universal form of expression, Leibniz ended up with a language of only two letters, but which is capable of transporting the deep meanings of the Chinese text (Loosen and Vonessen 1968). Through this work, which deals with ‘an alphabet of human thought’, and not only with a convenient two-letter alphabet, he remains still far ahead of all those in search of a universal language – which today seems to be that of the base-two binary alphabet. Work on the various aspects of representation prompts little recognition. This has to do with the old problem of acknowledging means versus acknowledging ends. Scientists from various domains made X-ray, MRI, and fMRI possible. But once these contributions were integrated in the new machines, the persons who made such technology possibly faded from history. That a new form of representation is a necessary, although not sufficient, condition for making computation possible is simply ignored. Otherwise, Leibniz’s computer would rank as the beginning of the age of computation, not as a historic curiosity.
Leibniz addressed representation because a lingua adamica ought to share in its means of representation. What made me assert (Nadin 1997a, 1997b, 1998) that Leibniz is the father of the digital – and thus, of the information age – is the powerful representation he chose, not so much to please a patron or to open access to Chinese writings, but to overcome the ambiguities of natural language. It was a rather fortuitous accident that my book (Nadin 1991), in which I introduced the notion of anticipation in relation to the mind, was published in the same series (Belser’s Milestones in Thought and Discovery) in which Leibniz’s binary system was made available to the scientific community. Were it not for the publisher’s initiative, scientists would have continued to ignore the original letter to the Herzog and the text on Chinese philosophy. My awareness of Leibniz has other roots, as well, among them, my interest in Charles S. Peirce.
3.1.2 Peirce’s semiotics
According to Bertrand Russell (1959, p. 276), Peirce was, ‘Beyond doubt [ . . . ] one of the most original minds of the later nineteenth century, and certainly the greatest American thinker ever.’ Still the most important American philosopher, Peirce proceeded in the same vein as Leibniz, elaborating his own considerations of computation (Peirce 1871). His semiotics, i.e. ‘a logic of vagueness’ (Nadin 1983), is in fact a comprehensive theory of representation and the associated interpretation. Peirce’s sign topology is meant to show how classes of signs correspond to classes of objects; and his sign operations correspond to classes of processes. The time dimension is implicit, in the sense that sign dynamics is interpretation dynamics, and the source of this dynamics is the interpretant process:
A representation is an object which stands for another so that an experience of the former affords us a knowledge of the latter. There are three essential conditions to which every representation must conform. It must in the first place like any other object have qualities independent of its meaning. It is only through a knowledge of these that we acquire any information concerning the object it represents. [ . . . ] In the second place, representation must have a real causal connection to its object. […] In the third place, every representation addresses itself to a mind. It is only in as far as it does it that it is a representation. The idea of the representation itself excites in the mind another idea and in order that it may do this it is necessary that some principle of association between the two ideas should already be established in that mind (Peirce 1873).
Like other mathematicians, Goldfarb (1997) is fully aware of the role semiotics plays in our understanding of representation. His contribution to the International Conference on Intelligent Systems and Semiotics is adequately entitled The Inductive Theory of Semiotic Systems. It is yet another record of the many ‘tributaries’ that ‘flow’ in the ambitious project for an inductive theory and practice of knowledge, which includes inductive computation. In the structural measurement theory, the role of semiotics is by no means formal if, in addition to number-based representations (already symbolic), ETS could make process representations available. Given my own long-term involvement with semiotic processes (semioses, as Peirce defines them), I found ETS compelling because it pursues the goal of providing formative aspects for the subject we try to understand.
3.1.3 Elsasser and natural experiments
It is at this juncture that the name of a distinguished physicist (a close collaborator of none other than Niels Bohr) should be brought into the picture if we want to put ETS in the proper frame of reference. Walter Elsasser (1998) undertook an attempt at a foundation of biological sciences, noticing (as did Erwin Schro ̈dinger 1944) that physics could only partially explain the living. Elsasser did not come up with an alternative representation, but advanced alternatives to what we call experiments, and thus to measurement, which is a dominant theme in Goldfarb’s ETS.
Observing that the reproducible outcome of experiments qualifies the measured/ represented system as stable, Elsasser draws attention to a class of unpredictable systems, such as those pertinent to the living, ‘whose future remains indeterminate from the physio- chemical point of view’ (1998, p. 143). The experimental method, built upon number- based measurement procedure, ‘has a strong built-in bias in favour of stable results’. The biological accepts a partial representation in terms similar to those of physics and chemistry; but as opposed to physics-specific entities, it begs an additional description of its peculiar condition. Elsasser went as far as to suggest the adoption of Niels Bohr’s concept of complementarity: ‘two different sets of order for inanimate and for living things’ would embody a ‘generalized complementarity’ (1998, p. 144). The ‘two types of order’ that ‘exist in the world’ are such that ‘they never contradict each other’. And he draws the following, revolutionary, conclusion:
… conventionally designed experiments cannot teach us anything beyond the fact that organisms are physio-chemical systems. If the holistic properties are to be verified experimentally, a different type of experiment from that conventionally used by physicists and chemists are required. (1998, p. 148)
It is not enough to ask only what the magnitude – i.e. number representation – of a variable is. We need to focus on correlations between various observables, ‘either on a given object or perhaps only on a class of objects’.
Elsasser’s conclusion should inform current research of living systems: ‘An epistemology of organic life that is free of internal contradictions cannot do without the idea that holistic transfer of information does occur in living organisms’. (1998, p. 149)
3.1.4 Rosen and measurement
With Robert Rosen, we get even closer to the fundamental contribution of structural measurement. Rosen is the mathematician of biology; this means that biological dynamics is his real focus. This is not the place to present Rosen’s monumental work in detail. So far, science has not been very kind to his legacy; nevertheless, his work deserves our utmost attention (Nadin 2010a). In these few notes, I shall refer less to his works on defining life and more to the intricate questions raised in Fundamentals of Measurement and Representation of Natural Systems (Rosen 1978) – unfortunately, ignored even by those active in the scholarship of measurement. The premise in Rosen’s book is simple:
Every recognition, measurement, discrimination, or classification ultimately rests on the capacity of a given system S to induce a dynamics (i.e., change of state) in another system, M
. . . variously called a meter, discriminator, recognizer, classifier, etc. (1978, p. 4)
Informed by relational biology (an area of studies associated with Rashevsky (1954), Rosen observed that the structure and organization of an adult organism evolves from an initial cell. Therefore, ‘the measurement problem in physics was the same as . . . pattern recognition’ (Rosen 1978, p. xvi). To measure is to extract a feature, based on which one recognizes a pattern.
Essential to our understanding of the living is the acknowledgement and representation of interactions. In the physical, the linkage between measurements is a vehicle for prediction. This makes science a form of ascertaining linkage relationships between observables (Rosen, p. 35). As linkage relationships among observables change, as new linkages are generated, and as others are modified or broken, we realize that the living has a different dynamics. Rosen noticed that there can be no ‘meter for reading probabilities’. The more observables we add, the more we affect the structure. Therefore, entropy becomes contingent and not intrinsic. Since the actual dynamics of a system is the expression of all interactions with the system, to represent the living is to identify the interactions resulting in the quality we call life.
3.2 ETS and some of its assumptions
Like Rosen, Goldfarb works in epistemology, focusing on the representation of dynamic
entities. This is what ETS is. Goldfarb’s fundamental thoughts are:
- classes exist in reality (realist view);
- all there is, is subject to change (Parmenides’ view); and
- formative history needs to be captured if we want to understand not only how things
are, but also how they were and eventually will be.
My initial attitude towards Goldfarb’s mathematics (as he likes to call it) was informed by my work in anticipation – impossible to even conceive of within a representation system slave to the tradition of the number system (i.e. quantitative description).
The historic context of the subject of representation automatically brought Leibniz and Peirce into the picture, while obsession with change, in particular change within natural systems, guided myself and my associates to the work of Elsasser and Rosen.
3.2.1 The concept of class
First a word of encouragement: neurophysiological studies in non-human primates make the role of classification evident (categorization of signals associated with classes of objects or activities, Gifford et al. 2005). It seems that it is simply more efficient to perform cognitive tasks at higher levels of abstraction or generality than in the realm of rich correctness. Furthermore, research was able to identify the neural correlates of categories and concepts (Miller et al. 2003). Animals, and human beings more so, can ‘detect basic characterizations of events and store them as generalized classes’.(Miller et al. 2003, p. 198) Beyond the specific details of sensory inputs and motoric output, we find a domain of generalizations that supports adaptivity.
Now the discouraging observation: there is no consensus whatsoever in defining a class. Actually, for the longest time, the word class stood for the word set. In Principia Mathematica (Whitehead and Russell 1997, first published in 1910), the arguments set forth refer to classes, sub-classes, etc. Mill and Boole used only class; and even translations (such as the German Menge) led to classes, not to sets.
Tracing the formative record of the word leads us to Pierre Gassendi (Institutio logica, 1658), and to Locke (Essay on Human Understanding, 1690) with the meaning of genus or species or universal. Boole referred, not very precisely, to Aristotle (the omni et nullo principle): ‘Whatever is predicated universally of a ,class. of things, may be predicated in like manner of any thing comprehended in that class.’ (Boole 1847, p. 18). For logicians, class soon becomes interchangeable with genus or species. von Neumann (1925) distinguished between classes and sets: every set is a class, but not conversely. In set theory, as it is practiced today, a class is a collection of sets that can be unambiguously defined by a property that all its members share. Some classes are sets (e.g. all even integers); others are not (e.g. the class of ordinal numbers, or the class of all sets). A class that is not a set is called a proper class. Schröder’s Calculus of Classes (1985) provides further details.
Still, maybe Goldfarb’s best option is to select a biologically inspired definition, since this is one of the major arguments in favour of his system. Whether it will be Linneaus ranks (cf. Systema Naturae) – Class, Order, Genus, Species, and Variety – or the more common classification that places Class below Phylum and above Order is still open. But to ignore the difficulty, under the assumption that because classes exist we do not need to identify them, is epistemologically unwise. Let us not ignore the fact that in object- oriented programming, classes group related variables and functions, while in games (those known as role-playing games or RPGs), they define a character’s archetype and career.
The effort to define classes, which is important when working with structural measurements, cannot ignore one of Elsasser’s major messages: classes in the physical realm are homogenous; classes in the living are heterogenous. Since a ‘theory is as good as the experiments that support it’ (Elsasser 1998, p.150), we shall have to look for both the quantitative and qualitative agreement between the reality and the representation. In the final analysis, anticipation embodies quantitative and qualitative aspects, impossible to reduce to each other, as they relate to the whole and not to some constitutive parts.
3.2.2 The concept of time
Anticipation cannot be understood without a good grounding in the knowledge of time. Since at the core of ETS is the formative history, i.e. the time sequence, it is justified to assume that time-related phenomena expressed in anticipation can be represented in the formalism it advances. Every piece of evidence we have acquired through the AnticipationScope confirms this basic assumption.
However, like class, time is by no means well defined. From the machine model advanced by Descartes, we inherited a representation of time as interval: homogenous, one-dimensional, one-directional, a continuum. Once we take a closer look at nature, we realize that there is more to time than the interval. As I considered anticipation, it became clear that real time and faster-than-real time are not metaphors, but the embodiment of different time scales. In defining the various levels at which structural processes take place, the ETS formalism addressed this issue. It is probably useful to look at the concept of time from a less deterministic and reductionist perspective. The various time scales identified in the functioning of the human body are only a suggestion of the richness of time. Consider the heartbeat, saccadic movements, the very fine tremor of our fingers as we touch something (which is the source of tactility), the clock at which neurons fire, the day-and-night cycle clock, etc. These are documentary evidence of the many ‘clocks’ at work in the organism. Synchronism gives depth to time, and thus we can talk of time perspective, and even parallelism. ETS will benefit from our progressively better understanding of time, if in defining its various components, those who apply ETS will leave it open enough to accommodate them. Interaction among entities living in different time frames is one of those subjects that only ETS could also define as a subject of gnoseological interest.
3.2.3 The generative component of ETS
Goldfarb is very respectful of Chomsky’s ‘concept of generativity’. (Goldfarb et al. 2007, p. 5) Inductive class representation and modelling inductive processes are, after all, the major themes of ETS. He is very clear about the need to clarify the nature of the connection between a class description (i.e. its representation) and the process that ultimately generates class objects. He goes even further and suggests the possibility of defining multi-levelled class generating processes. This is new territory, well defined by the powerful premise he articulates:
. . . the concept of structural object representation cannot be divorced from that of a generative object representation, i.e., that of a representation capturing the formative/generative history of the object. (Goldfarb et al. 2007, p. 7)
Chomsky’s (1966) generative grammars (part of formal grammars) do not explicitly [emphasis mine] encode formative aspects. But, as Goldfarb himself notices, ‘hidden behind a string representation’ (which is the Chomskian grammar representation), there are many formative histories. The string might be indeed inadequate for a structural representation in Goldfarb’s definition, but it proves useful in the deployment of relatively simple generative mechanisms.
For some reason, the work on the inductive structure for the ‘shape’ (Goldfarb and Golubitsky 2001, pp. 3ff) caused me to look back at mathematical contributions to the visual based on Chomsky’s grammar. Romanian mathematicians, prodded by Solomon Marcus, had a real love affair with formal languages. In particular, Paun’s (1982) attempt at defining two- and multi-dimensional grammars for generating decorative motifs impresses me as an elegant development in the spirit in which Goldfarb tries to overcome the initial string-based representation. (Paun 1982, pp. 204–205) On this note, I would also contrast Goldfarb’s generative approach to the representation of fairy tales (the early work of Vladimir Propp 1968) to Marcus’s (1978) generative procedures applied to folklore. (Marcus provides foundational contributions to linguistic-mathematical models, which still deserve our attention.)
I bring up these examples exactly because I recognize in Goldfarb’s system the frustration experienced by many scholars using generative grammars. But it turns out that some limitations can be overcome if the representation mechanism adopted is changed. In some ways, my remark points to a strength of ETS. It integrates the many questions we all have faced in dealing with limitations inherent in the mathematics of a reductionist tendency. An older attempt at transcending such limitations led to the adoption of pseudo- qualitative fuzzy set procedures. A two-dimensional fuzzy generative grammars as a form of inductive representation (Nadin 1986) served as means for describing flat images (landscape, artworks, etc.). The example of how the ordinary landscape of rural Ohio can be seen from an airplane or from a satellite as a Mondrian painting. The reciprocal holds true, as well: look at a Mondrian painting and you will recognize the grid structure of cultivated land. These examples served as a case study in a presentation to computer scientists focused exclusively on deterministic procedures. That is, I tried to demonstrate why we need PR procedures more subtle than those deployed in land surveys, and that to see something means to anticipate the image. This is, of course, consonant with vision research (Berry et al. 1999) of how images are formed on the retina. The brain does not receive data only through visual sensors. It generates its own data, and the result is the synthesis between information received from reality and information generated on account of previous experiences. The lecture also reported on Noll’s (1966) and Nake’s (1974) PR experiments and generative mechanisms. Fifteen years later, the anticipatory perspective advanced was confirmed. After the terrorist attacks on several major targets in the USA – recalled by the date 9/11 – many experts recognized that the need for new mathematics involved more than a formal representation of a work of art. The actual subjects were the application of fuzzy grammars for image generation, and inductive learning. When art and reality meet, we realize that a unified representational procedure, such as the one embodied in ETS, is an expression of knowledge characteristic of the human species, defined through its creativity.
3.2.4 The concept of information
Information – do we really know what it is? Goldfarb proposes a ‘new, informational view of the Universe’. (Goldfarb et al. 2007, p. 9) Nobody can take such a statement lightly. Still, very few (if any) will challenge it at its root. In the Information Age (as our age is almost unanimously labelled), everything is information. Chaitin (2004) with his algorithmic information theory – a scientific theory is a computer program that calculates observations –looks for legitimacy in Leibniz’s thinking. Many other scientists think that what reality does is to compute, i.e. to process information. Even Divinity has been brought into the discussion: is God a computer (Kelly 2002)? A programmer? (In the recent past, before the computer automated mathematics, God was a mathematician!) Wolfram’s (2002) principle of computational equivalence led him to rediscover the world through generative informational procedures based on cellular automata. In short, information and the appropriate information processing procedures are all we need.
Against this background, Goldfarb et al. (2007, p. 10) first asks, What is the informational structure of the Universe that allows for the emergence of biological information processing? He subsequently asserts a uniformity of the informational view of the Universe. He does so because otherwise, he could not avoid the traps attributed to vitalism:
Indeed, if biological species ‘invented’ fundamentally new forms of representation that have not previously existed in nature, then this is tantamount to saying . . . biological mechanisms themselves . . . cannot be understood on the basis of physical mechanisms. (2007, p.10)
This is exactly the point I want to make: biological mechanisms cannot be understood only (i.e. exclusively) on account of physics. Back to vitalism? No, but we need to acknowledge that, in the act of discarding vitalism, we gave up the scientific obligation to produce descriptions of the living that do not explain away what makes the living different from the non-living. For a very ambitious project, as ETS undoubtedly is, to ask such questions at the outset is unavoidable. Mathematics has a very good chance of succeeding where philosophy failed.
Our concept of information relies on a law in physics: the second law of thermodynamics (as elaborated by Clausius and eventually expressed by Boltzmann). Based on this foundation, Shannon (1948) derived a law describing the loss of information in the process of communicating a message. In reality, the Second Law in Shannon’s version, ‘holds for any natural process in which a system can be considered as closed with respect to some properties’. Moreover, as Elsasser showed (1998, pp. 136-137), ‘the observed stability of organic form and function, over many millions of years . . . ’ makes the information concept based on thermodynamics debatable with respect to its uniform application to both the physical and the living. I would go even further in arguing that, as opposed to physical entities, the living not only receives, processes, and outputs information, but also generates information (still within the concept of information used so far). This idea was brought up as we discussed an example of visual perception and how images are anticipated. Entropy only partially qualifies the dynamics of the whole. Boltzmann’s famous equation S = k log W, in which S stands for entropy, k is a constant (the Boltzmann constant), and the logarithm of the states of the system W has been reconsidered many times in recent years. Tsallis et al. (2000), among others, noticed that, under certain circumstances, some systems undergo a reduction in their entropy. Long before, Leo Szilard (1929), in describing biological processes, took note of the decrease in entropy in living systems. The new theory of disorder takes into consideration the dynamics of self-organization. For an information-based representational system, these observations about the not fully satisfactory definition of information are an invitation to improve upon the epistemological premises adopted.
An epistemology of the universe, such as ETS tends to be, has to be free of internal contradictions. For this to happen, those who work in structural measurement will eventually have to challenge the definition of information or to openly accept the Niels Bohr complementarity principle. How this principle can be translated into the procedures of ETS is not a trivial question. But in the long run, Goldfarb will not be able to escape addressing it. Just as we have for a long time dealt with non-linearity through reductions to linearity, we still deal with some aspects of the living as reducible to the non-living reality of physics. This expedient procedure buys us time, but it does not solve the matter of principle. A redefinition of information as it pertains to biological processes is unavoidable at this time. We might end up with two complementary definitions, or with one encompassing definition, within which the current definition is a particular case.
3.3 Pattern recognition (PR)
As a characteristic of the living, anticipation is an expression of its dynamics. Therefore, it is the ideal validation candidate for a representational system, such as ETS, that specifically attempts to capture change. If the tennis serve is within the speed and spin values that make its return possible on account of reaction, we can describe the successful action in terms of deterministic PR. And we can build a ‘return tennis serve’ AI machine that can help to coach players in need of increased reactive performance. The system would consist of sensors used to capture observations; a feature extraction procedure that actually processes the information encapsulated in observations; and a description procedure that classifies the observations, relying on the extracted features. Tennis coaches who make a living from producing future tournament winners already have such machines at their disposal. If someone skis downhill on slopes that allow for a maximum speed, at which reacting to obstacles and changing conditions is sufficient for successfully finishing one or several runs, we can do the same. The champions we see on TV were often trained in facilities with such PR implementations in virtual reality settings.
PR can guide chess players to a performance level where the next move is still only in reaction to the adversary. This is how many computer chess programs operate, and how the average player functions. At the foundation of such PR processes, we certainly recognize inductive learning and the associated representation. As we know, it all boils down to defining a function
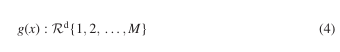
which represents a player’s assumption of y given x. The problem at hand is how we arrive at a good description of g, either in natural language, or in some other forms of expression, preferable in mathematical descriptions, that are computable. The mapping is called a classifier, and we tend to regard those who perform well – tennis players, skiers, chess players, as well as physicians and meteorologists – as having built-in high performance classifiers. Given the enormous size of the space x, classifiers end up being anything but perfect. However, for descriptions of the physical world, PR provides very convincing methods. Even for the living, in situations below the anticipation threshold, where reaction defines interaction, PR is a very powerful method.
However, if the interaction between the living systems described above is over the threshold of reaction, dynamic PR becomes necessary. Let us shortly observe that dynamic is a relative qualifier. Some will define probabilistic-driven PR (Devroye et al. 1996) as dynamic. The observation in such systems ends up being a d-dimensional vector x; the unknown nature of the observation is called class (yet another reason for Goldfarb to work on ‘dis-ambiguization’ of this fundamental concept); and what stands as a substitute for inductive learning is the frequency of encountering some pairs of x and y in a relation that can be formalized. Experts no longer work on producing classifiers, rather, they bring history (or ontologies) – data from the past that evinces some pattern – to AI programmers. That this is not formative history, which is Goldfarb’s subject, is obvious. Bayes classifies work like that. Statistical PR belongs to the same perspective. One can use Hidden Markov Models, which are a particular case of a stochastic finite state automaton. In other cases, such as when evolutionary natural objects were considered (Veyis et al. 2002), fuzzy Petri Nets were used. I bring up these as examples of what the PR community calls dynamic PR in order to make clear the dynamics referred to is well understood as pertaining to the deterministic domain.
Goldfarb is aware of these dynamic models. He is also inclined to integrate in his representation knowledge resulting from a stochastic perspective. There is no suggestion here that the epistemological view is wrong or inadequate; however, it is clear that, in addition to the inductive process, abductions, or hypothesis-driven learning, would have to be considered. There is no reason to doubt that Goldfarb can accommodate the need to account for abduction. Up to 1865, the common understanding in logic was that the so-called class of deductive arguments (also known as necessary inference) and the inductive arguments (probable inferences) covered the entire gamut. With Peirce, the class of probable inferences was further distinguished as inductive and abductive inferences (which he called hypotheses and retroductive inferences; Peirce 1905).
The suggestion I make at this time might prove beneficial for maintaining the goal of a unified representational system, which is Goldfarb’s goal. What abduction might supplant is the specific information that distinguishes the physical from the living, without denying the implicit realization of the biological in the material substratum. Goldfarb might find his own ways to account for the distinction, as well as to associate to PR, in its classical formulation, a complementary focus: dynamic recognition driven by data that associates probability and possibility.
4. ETS and the anticipatory profile®
We can examine anticipatory expression from the perspective of PR, or of dynamic systems – where anticipation looks like an attractor. We can consider anticipation as reverse computation – since in the living, the laws of thermodynamics need to be understood according to the condition of the living as an open system (metabolism dictates that energy be continuously taken in). We can think of anticipation as an expression of entanglement, though not at a quantum scale. What we cannot do is to avoid considering the dynamics of anticipation, how it changes over time. In other words, can it be that we are born with it, or is anticipation the product of nurture, i.e. of learning? The dynamics of anticipation is the record of its evolutionary and developmental change. Both dimensions are of interest to a structural representation. The change in anticipatory characteristics over the life of the living entity under consideration is part of its coming into being, and its eventual death. In many ways, it is the formative history of such an entity. In this sense, ETS is not only a good candidate in providing a representation, but a test case for our ability to gain knowledge about anticipation. Such knowledge will eventually inform much of the science and technology of our age. We have already learned a lot about the brain activity of the young during their ‘explosive’ hormonal phase; and we have learned quite a deal about how ageing affects anticipation in adults.
Awareness of anticipation probably dates back to questions asked about some individuals who outperform others in a context of ‘all things being equal’. I would prefer not to speculate on how this awareness is reflected in all kinds of descriptions. Survival implies anticipation. Let me succinctly point to two aspects: pregnancy, for instance, triggers increased anticipation (Russel et al. 2001), expressed in increased activity in the cingulated cortex. Recent data (Kinsley and Lambert 2006) document that pregnant rats are more effective, by a factor of 6, than virgin rats in navigating mazes and in capturing prey. In contrast to pregnancy as an expression of enhanced anticipation, ageing results in diminished anticipation. There is learning, inductive and abductive in nature, and loss of anticipation, each to be properly represented. For example, the anticipatory baroreflex decreases (Bowman et al. 1997). Older individuals get dizzy when getting up (even from a chair), and when the atmospheric pressure changes (Aikman 1997). This very often leads to a predisposition to stay in bed or to sit for longer periods of time, to passive habits (such as watching TV), and to avoid moving around. In such cases, dizziness is erroneously associated with activity, and a vicious, downward cycle begins. In this respect, our research aims to introduce forms of activity that will target an individual’s Anticipatory Profile (Nadin 2005).
More precisely, we want to build upon brain plasticity in order to stimulate the cognitive ‘rejuvenation’ of ageing individuals. This is the Seneludens project introduced at the beginning of this text (from senex, to grow old; ludens, associated with play), probably more suggestively described in G.B. Shaw’s observation: ‘We don’t stop playing because we grow old; we grow old because we stop playing.’ Three goals are pursued:
- assessment of each person’s anticipatory characteristics;
- recording their change over time; and
- testing if these characteristics are influenced by behavioural therapy, in particular,
involvement with a new category of games that engage the ageing in action (playing virtual tennis, even over the Internet with a partner, is an example; Nadin 2010b).
In order to accomplish this, we have to produce representations that will qualify our observations and actions. This is the context in which Seneludens meets ETS. This is also the context in which the AnticipationScope was elaborated. It is intended to provide the type of representation that is the object of ETS.
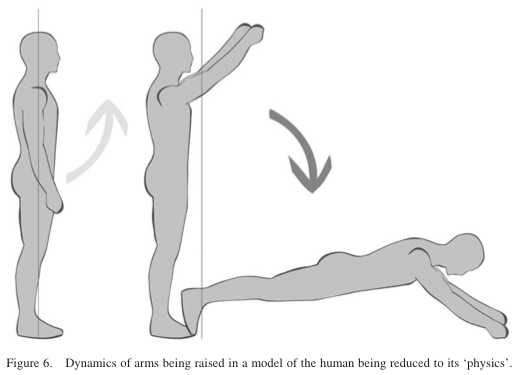
4.1 Leonardo da Vinci’s observation
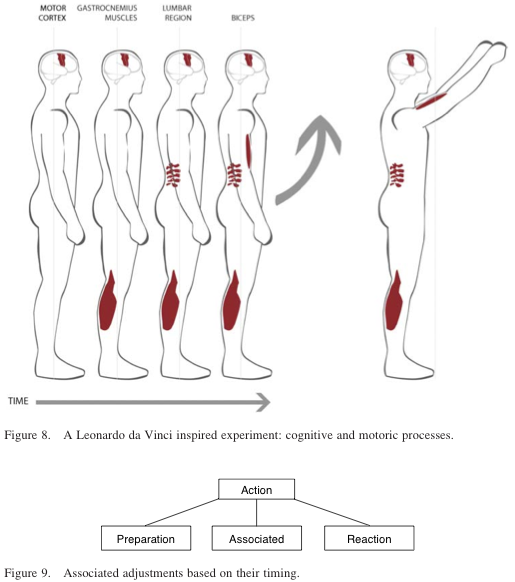
‘ . . . when a man stands motionless upon his feet, if he extends his arm in front of his chest, he must move backwards a natural weight equal to that both natural and accidental which he moves towards the front.’ Leonardo da Vinci made this observation in 1498, prompted by his study of motoric aspects of human behaviour. Five hundred years later, biologists and biophysicists addressing postural adjustment (Gahery 1987) proved that the compensation that Leonardo da Vinci noticed – the muscles from the gluteus to the soleus tighten as a person raises his arm – slightly precede the beginning of the arm’s motion. In short, the compensation occurred in anticipation of the action. Gahery makes it clear that every action (movements, tasks performed, etc.) involves ‘purposive’ and ‘non-purposive’ movement. This applies to postural adjustments (involving postural preparations, accompaniments, and reactions), or to gait dynamics, for example. Synergy comes into expression, as well as agonist (supportive) and antagonist (opposing) factors. Without anticipation, we would fall when we raise our arms. (Any object shaped like a human being, to which two arms of an equivalent weight are attached, could serve as a model; see Figure 6.)
Quite a number of researchers have tried to explain in detail how the anticipation that preserves our balance works. As already mentioned, ageing affects anticipation, and as we know from statistics, accidents connected to decreased equilibrium can result in fractures. The research carried out so far justifies the following statement: While it is true that old
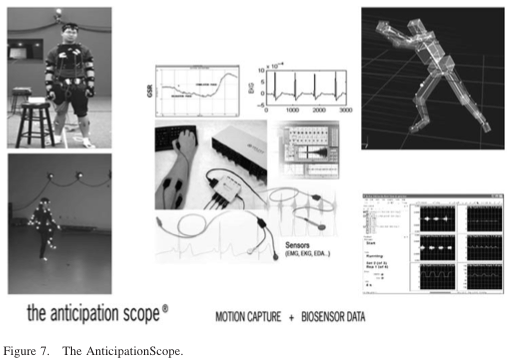
people, both women and men, break bones more often than others, it is not only because their bones are more fragile, i.e. decline of physical properties, but mostly because they no longer know how to fall. That is, they have a diminished anticipatory performance (Figures 7–9).
4.2 Measurements
To repeat: anticipation is expressed in action (Nadin 2007). Without proper understanding of this thesis, the qualifier anticipatory is misused. If we were to follow the tradition of scientific experiments, our observables would be nothing more than a mapping from the states of the observed entity – let us say the person raising his arms – to real numbers. Typically, state descriptions describe the system in isolation, and therefore they are incomplete. Their results could not be generalized for situations involving interactions. In terms of representation, equations of motion are nothing more than descriptions of how variables in the system change over time. The position of the arms could be seen as such variables. Different types of parameters (such as the ratio between body height and arm length, or the ratio between body weight and arm weight) and controls also enter the motion equation.
ETS which offers a different focus is fundamentally different: the compositional structure of objects or events. The output is no longer numbers, but a representation corresponding to a class plus the associated class transformation system, defined as structural class operations. The most important aspect is the necessary connection between the structural object representation and the generative object representation. Once interactions are considered – two individuals facing each other and raising their arms – the structured representation and the generative process change. The remainder of this article focuses on the experimental framework – the AnticipationScope that outputs an Anticipatory Profile – in which applications are currently carried out. Even if we could not
yet take full advantage of ETS, we look at the Scope as an embodiment of this multi- faceted meter able to capture the compositional structure of anticipatory processes.
The data acquired – i.e. integrated representations of movements and of associated physiological processes – would be at best confusing without the framework of its representation. The framework, as Goldfarb correctly noticed, guides the measurement. The sensors deployed so far were specified after careful consideration of the representation adopted. Each captures an aspect of the process. Their integration with the movement description – synchronized data streams that sometimes have different time scales – supports the inductive process that informs the explanation we are trying to submit to the scientific community on the nature of anticipation. It is no trivial matter to recognize, from a relatively large amount of data, what is associated with the holistic process, and what is actually a random variation. The events leading to the expression of anticipation (raising arms, for instance, in Leonardo’s example; or standing up from a horizontal position, with respect to the baroreflex) ultimately lead to stable structural processes. These are temporal sequences of interconnected basic events, taking place at different time scales. The global perspective (i.e. monotonic functioning over the life of the species) and the agents perspective embodied in observed processes are expressed in their unity. The traditional vector space and the syntactic description are of no help. Therefore, we looked for the ETS representation.
The following images should illustrate how the process eventually guides us in defining the measurement. Transformations will be further represented within the pictorial formalism of ETS without restating the theory behind it.
Gahery (1987) noticed that motoric acts are not localized events. ‘They belong to a whole set of physiological activities, including vegetative components and involvement of several muscles.’ He also suggested the following classification of the processes involved:
Let us be very precise: mind preparation precedes the raising of one’s arms by ca. 450–600ms. The subsequent muscle activity precedes the action by ca. 250–300ms. Accompanying actions – so far, three different motoric activities have been identified – follow the temporal scheme of the action itself. The reaction component (the action– reaction equivalent corresponding to Newton’s law of motion: ‘For every action, there is an equal and opposite reaction’) takes place shortly after the arms are raised and continues for the duration of the action. We proceed with:
- mapping from the physical entities involved (brain activity, muscle engagement, motoric expression, etc.) to the representational formalism (objects and their classes); and
- generative object representation.
The developmental history of each of the entities observed and the evolutionary history are considered in their unity. Due to the nature of the process, the multi-stage representational formalism (Figure 10) unfolds at different time scales. Let it be noticed that what we show in Figure 10 (inspired by Goldfarb) is rather suggestive of the multi- stage and change time scale than of the concrete representation of the postural adjustment described.
As we advance from one stage to the other, regularities are detected. And interestingly enough, we notice how ‘a future state’ (represented by the higher stage representation) influences a ‘previous state’ (arms raised and the mind processes associated with this). The possible future state, selected from among many other possibilities, exemplifies the specification of the degrees of freedom of the process.
The information view we obtain is the composite of movement description and pertinent sensors information. Based on our knowledge of currently deployed quantification methods, only an integrated AnticipationScope can achieve this dynamic representation of correlations resulting from many transformations. We are probably aware of only a few of them but hope to uncover more. The information process, in the classical sense of the term, drives the entire anticipation event.
The circles in the suggestive representation in Figure 10 stand for primitive transformations (what Goldfarb calls structs), which are connected in the process observed. At this time, the AnticipationScope works with two types of sensors (17 sensors altogether) and motion capture. As more kinds of sensors are deployed, more streams of transformation will be generated. Experiments carried out as recently as spring 2011 focused on the relationship between human performance and anticipatory characteristics (Nadin et al. 2011). Since each process represented has a different time scale, it is
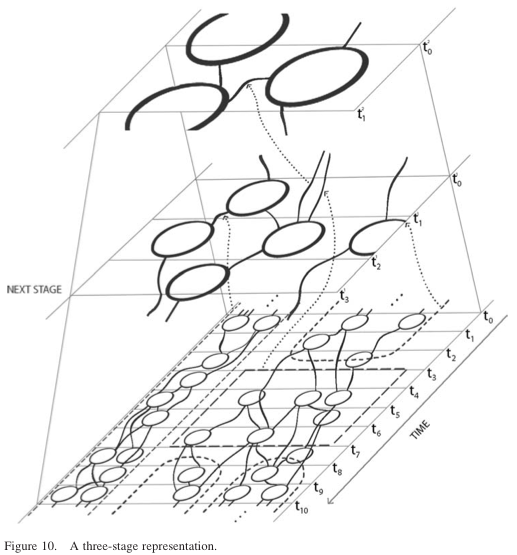
reasonable to expect several stages (not unlike those that Goldfarb represents in his paper, 2006a; see also Figure 10).
Generally speaking, the discovery of a new transform in the parallel process of measurement leads to expansion of the set of positives considered. Imagine that researchers could go beyond the macro-description suggested in Figure 10. That would involve brain imagery (or at least information pertinent to brain activity), and even information regarding the molecular level (as it pertains to triggering brain processes, muscle activation, and motoric changes). The real event –raising arms – and the associated events – as we define them at various interconnected levels – would lead to the ETS represented event that captures the entire dynamics of the action. But first we have to define the object environment (Figures 11–14).
According to Goldfarb, class generation takes place under the expectation of correlation between object and class representation. The appropriate class representation correlation remains to be further specified. We know that we have to define the primitives. These have the function of modifying existing classes, or of generating new classes. If

instead of raising arms, the person executes a genuflection accompanied by extending the arms horizontally, we will be dealing with a different class representation. Primitives correspond to single events; sensing (seeing, hearing, etc.) is continuously performed. The anticipatory expression – preparation for the event of raising the arms – is holistic: It integrates proactive model generation, selection among models, feed-forward process, feedback for balance control. Here are the events as they pertain to the anticipatory change we discuss.
Some elements are very tentative. For example: Is it possible to consider a brain in a context-free situation (i.e. autonomous control)? Probably not. Other elements are defined at relatively low-level resolution. In addition, integration of digital and analog must be pursued. The motoric is by all means rather analog than digital; that is, to a very high degree, continuity characterizes our movements. At this stage of our research, we are attempting only a tentative ETS presentation, a suggestion. The number of primitives will continuously increase as we learn more about the intricate nature of the anticipation process. Moreover, the nature of relations will require that we introduce qualitative differentiations, such as ‘some connection is stronger than another’, probably expressed in fuzzy terms. Eventually, all this can be represented visually, e.g. through a heavier line, or through multiple connections. The representation’s visual nature is conducive to a gestalt type evaluation: One can literally see how and what happens in the represented anticipatory action. This corresponds to the idiographic nature of anticipatory processes (cf. Nadin (2010c) on idiographic vs. nomothetic).
Let us attempt a first structural representation.
Mind states, i.e. brain activity, in correlation with the state of the motoric system, define the structural process. In every situation, the initial state is different; the final state – arms up and balance maintained – is, evidently, not a goal in itself, but a component of a more comprehensive action (e.g. catch a ball, greet someone, and indicate an emotional state). The structural representation, in which the system, driven by the process represented, adds new ‘knots’, has balance, in a dynamic sense, as output. What must be
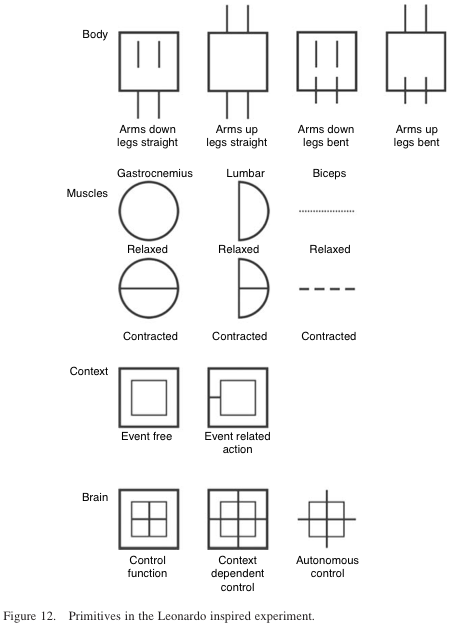
constantly determined is at which place in the process a new layer adds to the richness of representation. Based on such dynamic structural representations, we can formulate the following (which in the numeric measurement paradigm makes little sense):
Given a multi-level representation ![]() with the corresponding constituent level classes
with the corresponding constituent level classes ![]() and with partial specification generating system
and with partial specification generating system ![]() , we can assemble various
, we can assemble various
level n – 1 structs, associated or induced by an environment ![]() . Goldfarb warns that classes corresponding to lower levels ‘do not uniquely induce the topology of a next-level class’. (Goldfarb 2006b, p. 56) He points to the overall structure – what I called the holistic aspect – that ensures the uniques in the functioning ETS and the programming of the living.
. Goldfarb warns that classes corresponding to lower levels ‘do not uniquely induce the topology of a next-level class’. (Goldfarb 2006b, p. 56) He points to the overall structure – what I called the holistic aspect – that ensures the uniques in the functioning ETS and the programming of the living.

4.3 Pattern generation. ETS as programming
With all this in mind, let us entertain a speculative thought: why not consider ETS as a visual programming language, with the goal being programming anticipation as one form of interaction with the living? This would allow for pattern generation. We could define a set of desirable qualities, represented as output, construct the ETS that results in the function specified, and literally program, i.e. introduce a generative mechanism in the living entity subject to a programming effort. Rudimentary living forms could probably be a good starting point, since complexity does not reach the levels we encounter along the more developed expressions of life forms. Design might guide the entire process as we focus no longer only on representation, but on transformations (and their corresponding stages) that lead to expression. Multi-stage inductive structure comes into the picture; so does the need to complement it with abductive procedures. The action represented, i.e. ‘processes produced by various class generating systems can be subject to various transformations’ (Goldfarb 2006b, p. 59), can be affected by changes in the events or in the structure. As a matter of fact, ETS is a generative representation that overcomes the constraints inherent in Chomsky’s grammars. ETS could be considered a high-level programming language that can make anticipatory computing possible. Transformations apply to all levels. Given a concrete goal, we could examine (as we did with the example
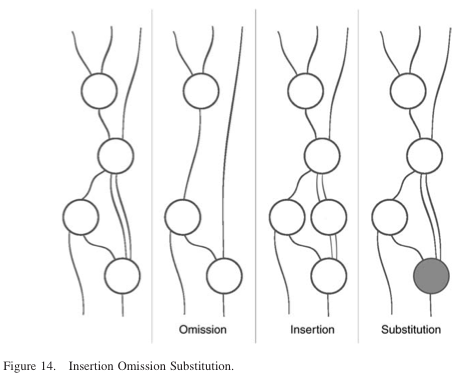 from Leonardo) the struct representation and define the additional information about the object and processes involved. The next step would be to evaluate each component and eventually ‘reprogram’ the whole by using insertion, omission, and substitution procedures for affecting the outcome of the process.
from Leonardo) the struct representation and define the additional information about the object and processes involved. The next step would be to evaluate each component and eventually ‘reprogram’ the whole by using insertion, omission, and substitution procedures for affecting the outcome of the process.
All these simplified ETS representations have the same final object, but the generative path is different. How the concrete anticipatory programming task will be performed is not the subject of these comments. However, anticipatory computing is a form of the non- deterministic computation immanent in the living (Nadin 2010d). The natural computation – information processing according to a variety of inter-related non- deterministic programs – can be represented. Alternative natural computations can be designed and implemented using the powerful representation of ETS. Goldfarb noticed that many concerns (such as comparing the performance of ETS to currently practiced representations, such as neural networks) would eventually have to be addressed, but in language specific to ETS. Construction of a class representation from a small training set for the class (Goldfarb 2006b, p. 66) proves to be useful in formulating the goal of effectively programming the living. This can take place not through the currently attempted (and so far unsuccessful) syntactic manipulation under the expectation of deterministic procedures, but by a semantically or pragmatically driven generation effort. The explicit transform concept required for this is probably still in elaboration. One can only hope that the scientific community will take the challenge and further contribute to the validation of ETS.
5. Conclusion
Fundamentally, we are in a context of interactivity, marked by our ability to adjust the representation, to keep it as individualized as possible. This is an empirical setting in which Pythagorean number-based mathematics is effectively complemented by the empirical testing of behaviour. The representation advanced by Goldfarb reflects, at least partially, the nature of human reasoning, which happens to be intrinsically richer than the number-based rationalist model of thinking.
Note
Anticipatory Profile and AnticipationScope are registered trademarks belonging to Mihai Nadin.
Acknowledgements
This work would not have been possible without the cooperation of all members of antE Ì – Institute for Research in Anticipatory Systems. Let me acknowledge the contribution of Dr Navzer Engineer (2005-2008), Cassandra Emswiler, Dr Gaurav Prahdan, Nathan Felde, and Dr Jeffrey V. Nickerson. Over the years, Dr B. Prabhakaran and Dr Sandra Chapman have provided valuable input. Funding for this work was provided by the University of Texas at Dallas, antÉ Institute for Research in Anticipatory Systems, and the Deutsche Forschungs Gemeinschaft (DFG). Leibniz’s memorial coin is reproduced with the kind permission of the Gottfried Wilhelm Leibniz Bibliothek (Hannover, Germany).
Notes on contributor
 Mihai Nadin’s interests and professional life combine engineering, mathematics, digital technology, semiotics, mind theory, and anticipatory systems. He holds advanced degrees in Electrical Engineering and Computer Science and a post-doctoral degree in Philosophy, Logic and the Theory of Science. His book, Mind – Anticipation and Chaos, introduced original ideas in the fields of mind and education (which later independent studies confirmed). Research in dynamic systems and the mind (Stanford University) led Nadin to probe anticipatory systems. Research at UC, Berkeley, led to several articles (e.g. ‘Anticipation – A Spooky Computation’, ‘Anticipating Extreme Events: the need for faster-than-
Mihai Nadin’s interests and professional life combine engineering, mathematics, digital technology, semiotics, mind theory, and anticipatory systems. He holds advanced degrees in Electrical Engineering and Computer Science and a post-doctoral degree in Philosophy, Logic and the Theory of Science. His book, Mind – Anticipation and Chaos, introduced original ideas in the fields of mind and education (which later independent studies confirmed). Research in dynamic systems and the mind (Stanford University) led Nadin to probe anticipatory systems. Research at UC, Berkeley, led to several articles (e.g. ‘Anticipation – A Spooky Computation’, ‘Anticipating Extreme Events: the need for faster-than-
real-time models’) and the book, Anticipation – The End Is Where We Start From (setting a foundation for the field in lay terms). He established the antÉ Institute for Research in Anticipatory Systems (2002) as a research, ‘think tank’, and consulting entity (for technical innovation, business, policy development, game-based simulations, defense). It became part of the University of Texas at Dallas (2004), when Dr Nadin accepted its invitation to become Ashbel Smith University Professor. Dr Nadin is carrying out research on capturing anticipatory characteristics on the AnticipationScope® . The Project Seneludens focuses on developing devices to maintain the anticipatory capabilities of the ageing population. Recent publications on anticipation include: An Integrated Mobile Wireless System for Capturing Physiological Data Streams during a Cognitive- motor Task: Applications for Ageing Motions (2007); Anticipation and Risk – from the inverse problem to reverse computation (2009); Play’s the Thing. A wager on healthy ageing (2010); Anticipation and Dynamics (2010, which won the best issue award of the IJGS). During the 2011– 2012 academic year, he will pursue research in anticipatory systems at the Hanse Wissenschaftskol- leg (Institute for Advanced Studies), Germany. For more information, see www.nadin.ws and www.anteinstitute.org.
References
Aikman, H., 1997. The association between arthritis and the weather. International journal of biometeorology, 40 (4), 192–199.
Berry, M.J. II, Brivalou, I.H., Jordan, T.A. and Meister, M., 1999. Anticipation of moving stimuli by the retina. Nature, 398 (6725), 334–335.
Boole, G., 1847. The mathematical analysis of logic, being an essay towards a calculus of deductive reasoning. London/Cambridge: MacMillan, Barclay and MacMillan.
Bowman, A.J., et al., 1997. Baroreflex function in sedentary and endurance-trained elderly people. Age and ageing, 26 (4), 221–224.
Chaitin, G.J., 2004. Leibniz, information, math and physics. In: W. von Löffler and P. Weingärtner, eds. Wissen und Glauben/Knowledge and Belief. Akten des 26. Internationalen Wittgenstein- Symposiums 2003. Vienna: O ̈BV & HPT, 277–286.
Chomsky, N., 1966. Topics in the theory of generative grammar. The Hague: Mouton.
Davies, C.W.P., 2004. John Archibald Wheeler and the clash of ideas. In: J.D. Barrow, C.W.P. Davies and C.L. Harper, eds. Science and ultimate reality. London: Cambridge University Press, 3–24.
Descartes, R., 1637. Discours de la méthode pour bien conduire sa raison, et chercher la vérité Ìdans les sciences. Leiden: Ian Maire.
Devroye, L., Györfy, L., and Lugosi, G., 1996. A probabilistic theory of pattern recognition. New York/Heidelberg: Springer.
Dubois, D.M., 1996. Hyperincursive stack memory in chaotic automata. In: A.C. Ehresmann, G.L. Farre and J.-P. Vanbreemersch, eds. Actes du symposium ECHO (Emergence – Complexite Ì Hie Ìrarchique – Organisation): Modèles de la boucle évolutive. Amiens: Université Ìde Picardie Jules Verne, 77–82.
Efroni, S., Harel, D., and Cohen, I.R., 2005. Reactive animation: realistic modeling of complex dynamic systems. IEEE computer, 38 (1), 38–47.
Elsasser, W., 1998. Reflections on the theory of organisms. Holism in biology. Baltimore, MD: Johns Hopkins University Press.
Gahery, Y., 1987. Associated movements, postural adjustments and synergy: some comments about the history and significance of three motor concepts. Archives italiennes de biologie, 125, 345 – 360.
Gifford, G.W. III, et al., 2005. The neurophysiology of functionally meaningful categories: macaque ventrolateral prefrontal cortex plays a critical role in spontaneous categorization of species- specific vocalizations. Journal of cognitive neuroscience, 17. Cambridge: MIT Press, 1471 – 1482.
Goldfarb, L., 1997. The inductive theory of semiotic systems. In: Proceedings of the 1997 international conference on intelligent systems and semiotics: a learning perspective, 22–25 September 1997. Gaithersburg: NIST Special Publication, 111–116.
Goldfarb, L., 2006a. Can a new representational formalism unify cognitive science? Special Seminar. Cambridge: Massachusetts Institute of Technology.
Goldfarb, L., 2006b. The first class(ification)-oriented representational formalism. Do you know what a class is? National Research Council of Canada, Institute for Information Technology, Colloquium Series 2006–2007, September 28, 2006. Available from: http://www.cs.unb.ca/~goldfarb/ETS_Lab/IIT-2006.ppt [Accessed 12 December 2010].
Goldfarb, L. and Gay, D., 2006c. What is a structural representation? A proposal for a representational formalism (fifth variation) [online]. University of New Brunswick, Canada. Available from: http://www.cs.unb.ca/profs/goldfarb/ets5/ETS5.pdf [Accessed 25 November 2006].
Goldfarb, L. and Golubitsky, O., 2001. What is a structural measurement process? Technical Report TR01-147. Faculty of Computer Science, University of New Brunswick, Canada.
Goldfarb, L., Golubitsky, O. and Korkin, D., 2000. What is a structural representation? Technical Report TR00-137. Faculty of Computer Science, University of New Brunswick, Canada.
Goldfarb, L., et al., 2007. What is a structural representation? Proposal for an event-based representational formalism, sixth variation [online] Technical Report TR07-187, Faculty of Computer Science, University of New Brunswick. Available from: http://www.cs.unb.ca/~goldfarb/ETSbook/ETS6.pdf [Accessed 11 November 2010].
Kelly, K., 2002. God is the machine. Wired, 10 (12) [online]. Available from: http://www.wired. com/wired/archive/10.12/holytech.html [Accessed 27 April 2010].
Kinsley, C.H. and Lambert, K.G., 2006. The maternal brain. Scientific American, 294, 72–79.
Kirchheim, H.R., 1976. Systemic arterial baroreceptor reflexes. Physiological review, 56, 100–177.
Loosen, R. and Vonessen, F., eds, 1968. Leibniz, G.W. Zwei Breife ü ber das binäre Zahlensystem und die chinesische Philosophie. Stuttgart: Belser Presse.
Marcus, S., 1978. Les modèles linguistico-mathématiques et la sémiotique du folklore (Linguistic-mathematical models and the semiotics of folklore). In: S. Marcus, ed. La Sémiotique Formelle du Folklore [Formal Semiotics of Folklore]. Paris: Éditions. Klincksieck, 1–18.
Miller, E.K., et al., 2003. Neural correlates of categories and concepts. Current opinion in neurobiology, 13, 198–203.
Montgomery, R., 1993. Gauge theory of the falling cat. Fields institute communications, 1, 193 – 218.
Nadin, M., 1977. Sign and fuzzy automata. In: M. Bense, ed. Semiosis. Stuttgart: AGIS Verlag, 19–26.
Nadin, M., 1983. The logic of vagueness and the category of synechism. In: E. Freeman, ed. The relevance of Charles Peirce. La Salle, IL: The Monist Library of Philosophy, 154–166.
Nadin, M., 1986. G-pictures: elements of a probabilistic pictorial grammar. Computer and Information Science Lectures and Seminars, Ohio State University, Columbus, 29 May 1986. Available from: https://www.nadin.ws/index.php?s1â„4G-pictures [Accessed 12 December 2010].
Nadin, M., 1991. MIND – anticipation and chaos. Stuttgart/Zü rich: Belser Presse.
Nadin, M., 1997a. The civilization of illiteracy, Dresden: Dresden University Press [online]. Available from:
Nadin, M., 1997b. Cognitive aspects of visualization, 1 [online]. University of Muenster, Germany. Available from: geoinformatik_online, Ausgabe 1/97, http://www.gio.uni-muenster.de [Accessed 8 September 2010].
Nadin, M., 1998. What kind of sign is a bit? [online]. Lecture: Semiotics and the Information Sciences, Victoria College, University of Toronto, October 13 – 15, 1998. Available from: http:// www.nadin.name/lectures/lectures_text/what-kind/what_kind.html; and https://www.nadin.ws/ archives/605 [Accessed 2 October 2010].
Nadin, M., 2003. Anticipation – the end is where we start from. Basel: Lars Mü ller Verlag.
Nadin, M., 2005. Quantifying anticipatory characteristics. Proposal submitted to the National Science Foundation (NSF–05.4746), Human and Social Dynamics: Dynamics of Human Behavior.
Nadin, M., 2007. Anticipation and risk – From the inverse problem to reverse computation, Paper presented at: ICDRIA (International Center for Decision and Risk Analysis) conference Decision-Making Under Uncertainty (A. Bensoussan, Organizer), School of Management, University of Texas at Dallas, May 21–22, 2007. Printed in M. Nadin, ed., Risk and decision analysis 1 (2), 2009. Amsterdam: IOS Press, 113–139.
Nadin, M., ed., 2009. Risk and decision analysis, 1(2). Amsterdam: IOS Press.
Nadin, M., 2010a. Anticipation and dynamics: Rosen’s anticipation in the perspective of time. Special issue of International journal of general systems, 39 (1), 3–33.
Nadin, M., 2010b. Play’s the thing. A wager on healthy aging. In: J. Cannon Bowers and C. Bowers, eds. Serious game design and development, 150 (28)8. Hershey, PA: IGI, 150–177.
Nadin, M., 2010c. A science of change. In: F. Chorda, ed. Vivir es cambiar. Barcelona: Anthropos, 127 – 166.
Nadin, M., 2010d. Anticipatory computing: from a high-level theory to hybrid computing implementations. International journal of applied research on information technology and computing (IJARITAC), 1 (1), 1–27.
Nadin, M., et al., 2011. Performance Scope, poster session at Body Sensor Networks (IEEE conference) Dallas TX, May 23-25, 2011. Note: It is only fair to list the participating students from the class Computational design: Inventing the future: R. Fuentes, W. Howell, M. Keiser, A. Lagow, C. Moezzzi, J. Seime-Rave, J. Warner.
Nake, F., 1974. Ästhetik als Informationsverarbeitung. Vienna/New York: Springer.
von Neumann, J., 1925. Eine Axiomatisierung der Mengenlehre. Journal fü r die reine und angewandte mathematik, 154, 219–240.
Noll, M., 1966. Computer Composition with Lines, 1964; see Human or machine – a subjective comparison of Piet Mondrian’s ‘Composition with Lines’ and a computer-generated picture. The psychological record, 16. Murray Hill, NJ: Bell Telephone Laboratories, 1–10. Downloaded by [Institutional Subscription Access] at 07:13 11 October 2011
Paun, G., 1982. Gramatici bidimensionale. Un model pentru generarea unor motive decorative folclorice [2-dimensional grammars. A model for generating decorative folkloric motifs]. In: S. Marcus, ed. Semiotica matematica a artelor vizuale (The mathematical semiotics of visual arts). Bucharest: Editura Stiintifica si Enciclopedica, 203–221.
Peirce, C.S., 1871. Obituary of Charles Babbage. The nation, 13, 307–308.
Peirce, C.S., 1873. On representations, MS 389 [online]. University of Perpignan, France. Available from: http://www.cspeirce.com/menu/library/rsources/76defs/76defs.htm [Accessed 5 November 2010].
Peirce, C.S., 1905. The varieties and validity of induction, MS. “G”. In: C. Hartshorne and P. Weiss eds., The collected papers of Charles Sanders Peirce. Vol. 2. Cambridge: Harvard University Press, 755–772.
Propp, V., 1968. Morphology of the Folktale. L. Scott, trans. 2nd ed. Austin: University of Texas Press.
Rashevsky, N., 1954. Topology and life: in search of general mathematical principles in biology and sociology. Bulletin of mathematical biophysics, 16, 317–348.
Rosen, R., 1978. Fundamentals of measurement and representation of natural systems. General systems research series, 1. Amsterdam: Elsevier Science.
Rosen, R., 1985. Anticipatory systems. Philosophical, mathematical, and methodological foundations. Oxford: Pergamon Press.
Rosen, R., 1991. Life itself: a comprehensive inquiry into the nature, origin, and fabrication of life. New York: Columbia University Press.
Russell, B., 1959. Wisdom of the west. New York: Crescent Books.
Russell, J.A., et al. eds, 2001. The maternal brain: neurobiological and neuroendocrine adaptation and disorders in pregnancy and post-partum. Dordrecht: Elsevier.
Schröder, E., 1895. Vorlesungen ü ber die Algebra der Logik (exacte Logik). Algebra und Logik der Relative, Erste Abteilung [Lectures on the algebra of logic (exact logic). Algebra and logic of the relative, 3. Leipzig: B.G. Teubner, 1.
Schrödinger, E., 1944. What is life? Cambridge: Cambridge University Press.
Shannon, C.E., 1948. A mathematical theory of communication. Bell system technical journal, 27, 379–423 and 623–656.
Szilard, L., 1929. Über die Entropieverminderung in einem thermodynaischen system bei Eingriffen intelligenter Wesen. Zeitschrift fü r Physik A, 53, 840–856. See also: On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Behavioral Science, 1964, 4, 301–310.
Thomson, A., ed., 1996. La Mettrie: machine man and other writings. Cambridge: Cambridge University Press.
Tsallis, C., et al., 2000. Generalization to non-extensive systems of the rate of entropy increase: the case of the logistic map. Physics letters A, 273.
Veyis, G., Loomis, P. and Menard, M., 2002. A fuzzy petri net for pattern recognition: application to dynamic classes. Knowledge and information systems, 4 (1), 112–128.
Whitehead, A.N. and Russell, B., 1997. Principia mathematica to #56. 2nd ed. Cambridge Mathematical Library. Cambridge: Cambridge University Press.
Wolfram, S., 2002. A new kind of science. Champaign, IL: Wolfram Media.
Zadeh, L.A., 1978. Fuzzy sets as the basis for a theory of possibility. Fuzzy sets and systems, 1, 3 – 28.
Posted in Anticipation

 Disrupt Science: The Future Matters
Disrupt Science: The Future Matters