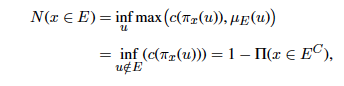in Risk and Decision Analysis (M. Nadin, Ed.), 1 (2009) Amsterdam: IOS Press, pp. 113-139.
PDF

http://content.iospress.com/articles/risk-and-decision-analysis/rda09

Abstract.
Risk assessment is relevant only if it has predictive relevance. In this sense, the anticipatory perspective has yet to contribute to more adequate predictions. For purely physics-based phenomena, predictions are as good as the science describing such phenomena. For the dynamics of the living, the physics of the matter making up the living is only a partial description of their change over time. The space of possibilities is the missing component, complementary to physics and its associated predictions based on probabilistic methods. The inverse modeling problem, and moreover the reverse computation model guide anticipatory-based predictive methodologies. An experimental setting for the quantification of anticipation is advanced and structural measurement is suggested as a possible mathematics for anticipation-based risk assessment.

Keywords: Anticipation, risk, prediction, inverse problem, reverse computation, structural measurement, anticipation scope, anticipatory profile

1. Statement of goals

Successful anticipation mitigates risk. This relatively innocuous statement, which somehow promises a world of reduced risk on account of effective anticipation, is of little use unless we define our terms. Indeed, although risk considerations go back as far as reflections on danger and chance in the ancient world, and anticipation, in some way, is acknowledged in antiquity, neither of them are defined and used in a consistent manner. There is a lot of accumulated evidence in respect to how people conduct their affairs understanding the implication of associated risk, or in respect to anticipating the consequences of their actions. But in the final analysis, the conceptual foundation for both risk and anticipation is at best preliminary. In respect to risk,¹ the many specializations – in mathematics (with a focus on probability and prediction), engineering, statistics, law, insurance and investment, for example – resulted in a variety of understandings. In addition, the psychology of risk (and the associated decision theory), the ethics, the politics, and the economics of risk have given rise to quite a bit of theoretic and applied work, but without a conceptual consensus on the meaning of risk.

Anticipation² is less well understood. Since Rosen’s [29] and Nadin’s [19] foundational work – one grounded in a structural view of the living, the latter on brain science – the major contributions have focused on cognitive aspects and on the possibility of somehow computing anticipation (see, for example, Computing Anticipatory Systems, CASYS, headquartered in Liège, which publishes the proceedings of its international conferences held every two years). As far as the relation between risk assessment and anticipation is concerned, we are practically in virgin territory. Therefore, we need to develop the conceptual framework, clarify language, and suggest ways to apply available knowledge, in full awareness of the need to develop, at the same time, criteria for evaluation.

It is the intention of this study to address these objectives. We shall proceed by defining the expectations of prediction as the ultimate goal. In further addressing the epistemological condition of the concepts of risk and anticipation, we shall be in the position to distinguish classes of risk, and to see at which juncture anticipation and risk can be meaningfully examined as somehow linked. We will have to extend the analysis to the context in which our description of reality makes possible and necessary the understanding of risk and, subsequently, of anticipation. The distinction between nomothetic – as it pertains to generality and law – and idiographtic – as it pertains to event sequences and to individuality – in other words, between science and history, will draw our attention because risk and anticipation share in their mixed epistemological condition. Only this fundamental understanding can help us explain
why probability-driven risk models remain partial as long as the possibilistic perspective is only marginally accepted. Anticipation studies, still in search of a consubstantial mathematical representation, are in the same situation.

Finally, in order to provide the expected predictive performance, we need to address the expectation of expressing risk and anticipation in ways that quantify both their qualitative and structural aspects. The inverse problem perspective and the associated reverse computing model are an attempt to suggest practical solutions. The Anticipatory Profile™, which is also a risk profile, is an implementation that has afforded good experimental results. I am aware that this statement of goals practically suggests a book. It might well be that this study is the first step towards that end.

2. Prediction and complexity

Science is rewarding in many ways. From the multitude of values it returns, predictions are the most important. This is true regardless of the scientific method: start with observations and build upon them until a theory results that can predict future observations; or start at the highest level of generality (abstract theory) and see how observations confirm it, thus making possible informed actions based on such a theory. As we advance in our understanding of change (dynamics, as change is also called), and as we improve methods of observation and their perspective, we notice that at times a wrong prediction falsifies a theory [26], and we need to start over. The history of science would be discouraging if we were to take the immense number of falsified instances as its main outcome. Actually, as yet another proof of the progress made over time in understanding the world we belong to, and ourselves in interaction with each other, the discarded is not a junk pile, but fertile ground for new inquiry.

We shall not, however, deal with science in general, but rather with anticipation – a characteristic of the living – and with risk – associated with human action toward a desired outcome. More precisely, we shall focus on successful predictions pertinent to anticipatory processes and risk assessment. We want to see how our understanding of anticipation and risk begs for better theories, which in turn might inform better predictions. Given the economics associated with risk assessment, risk management, and, in a broad sense, anticipation, predictions are enormously important. However, the expectation of prediction cannot be the only driving force of science. Rather, as we advance in unknown territories, where chances and risks reach a scale never encountered before, prediction becomes at best tentative, if not impossible. Almost all predictions – euphoric or utopian proclamations of chances, or depressing warnings of unbearable consequences – that have accompanied scientific breakthroughs in the last 100–150 years, proved undeserving of the attention they received from the public or from scientists. One can suspect that the famed Chinese proverb – “It is difficult to predict, especially the future” – is nothing but an expression of self-irony (sounding very much like one of Yogi Berra’s famous predicaments).

2.1. The forward problem and the inverse problem

Using a theory, complete or partial, for predicting the results of observations corresponds to addressing the so-called forward modeling problem. Alternatively, we can start out from measurements in order to infer the values of the variables representing the system we are examining. This possibility, called the inverse modeling problem in mathematics, is very attractive, since over time data has accumulated from instances of risk expression or from successful anticipations. Let O (i.e., the organism we are trying to describe) be the living system. The methodology we suggest is rather straightforward:

1. Parameterization of O, that is, submitting a minimal set of model parameters whose value characterizes the organism from the perspective pursued (for instance, neurological disorders or assessment of adaptive capabilities). This step is always based on prior knowledge, i.e., inductions. If the focus is on anticipation, the variables correspond to proactive components of action and interaction.
2. Forward modeling, that is, submitting hypotheses in the form of rules for the organism’s functioning such that for given values of the parameters, we can make predictions about the measurement results of some of the observable parameters. In a way, this is the same as establishing the linkage of quantified parameters. Therefore, it is also an inductive process.
3. Inverse modeling, that is, processing of inference from measurement results to current values of the parameters. This is, by necessity, a deductive process. The living, by many orders of magnitude more complex than the physical, evinces the strong interdetermination of these methodological steps. (Feedback is but one of the processes through which they influence each other.) Let’s take note of the fact that the choice of parameters is neither unique nor complete. We can compare two parameterizations to find out if they are partially or completely equivalent. This is the case if their relation is through a bijection (one-toone mapping). Furthermore, we can generalize a space of many models through a manifold. The set of experimental procedures that facilitate the measurement of the quantifiables characterizing the organism is the result of applying a quantifying (measurement) algorithm.

Finally, let us be aware that the number of parameters needed to describe a fairly complex organism is, for all practical purposes, infinite. However, in many cases, a limitation is introduced such that the continuity aspect of the living is substituted (or approximated) through a discrete set of parameters. Moreover, even such parameters can take continuous values (mapping to quantities expressed through real numbers) or discrete values (integer numbers). Further distinctions arise in respect to the linearity of the model space (the consequence affects the rules for model composition, such as the sum of two models, multiplication, etc.).

2.2. Causality

The procedure described above can be applied to any system, but our focus on the organism (the living) corresponds to the fact that anticipation is a characteristic of the living.

Since the time Descartes set forth his reductionist-deterministic perspective, physics has claimed to be the theory of all there is, living or not. Causality, in Descartes’ understanding, is based on our experience with the physical world. The cause-and-effect sequence characteristic of the reductionist deterministic understanding of causality ensures that the forward problem has a unique solution. This guarantees the ability to make predictions regarding the dynamics of such phenomena. Obviously, this does not apply to quantum phenomena. If, however, causality itself is subjected to refinement – as in quantum mechanics, but not only – even the forward problem no longer results in a unique solution. Predictions become difficult; therefore, risk considerations are at best tentative.

Direct problem formulations are a description of the effect connected to a cause. In the inverse problem, the situation is reversed.We look for the existence, uniqueness, and stability of the answer to the problem that describes a physical phenomenon defined as an effect of something we want to uncover as its possible cause. The inverse problem, even with causality restrictions in place, has a plurality of solutions; that is, different models predict similar results. Or, if the data is not consistent – which often happens in the realm of the living – there is no solution at all.

With all these considerations in mind, it is easy to notice that the reductionist-deterministic description corresponds to a modeling of the world in a manner that allows us to infer from a lower complexity (that of the model) to a higher complexity (that of real phenomena). This kind of mapping is quite handy for a vast number of applications.We can state, as a general principle – in opposition to reductionism – that the higher the complexity of a system, the more reduced our chances to map it to a low-complexity model. Consequently, the predictive performance of modeling high complexity phenomena through models of lower complexity is reduced. As a human endeavor of implicit epistemological optimism, science cannot take this situation as a curse and ignore the reality of high complexity. This is the challenge: to increase predictive performance relevant to complex entities by a more adequate understanding of their condition.

3. How do we acquire knowledge of risk? How do we understand anticipation?

With these thoughts regarding prediction in mind, we shall examine the epistemological condition of anticipation and of risk, as well as their interrelationship. Based on such an attempt to advance some coherent theories, we shall return to the concrete aspects of the inverse problem as it concerns anticipation and risk. Eventually, we shall generalize it in regard to reverse computation – which embodies the inverse problem in computational form – and pose the question of whether alternative descriptions, not grounded in the exclusive representation of quantity-based observations, are a better way to examine anticipation and risk. One particular aspect – the Anticipatory Profile – will guide us towards predictive models of the individual. The risk associated with the change in the Anticipatory
Profile (e.g., neurodegenerative disease, drug addiction, aging) will be specifically addressed as an illustration of the perspective advanced.

Anticipation is usually associated with successful actions – high performance (in sports, military operations, education, marketing) – or avoidance of negative outcome (in the market, in preventing accidents and injuries). Successful choices (related to tactical decisions, art and design, diagnostics) are always risky choices. For a starter, this is how anticipation and risk are related. As such, anticipation is an underlying factor of evolution, expressed in the ability to cope with the extreme dynamics of the natural world and of society. Resilience³ [33] cannot be ignored; but in the long run, what wins is the successful adaptive capability of individuals and of species, which is the expression of anticipation. Biological processes that inform the living about how to cope with change before change occurs is a good description of what makes anticipation possible.

Resilience is about coping with change (in weather conditions, in service delivery, in a variety of situations affecting the market, among many more examples). Anticipation is about succeeding in a world of change. The tennis champion does not return equally successfully all the fast serves from the opponent; the ski champion does not always make it down steep slopes in the shortest time (sometimes not at all); we sometimes stumble as we walk over less than flat terrain, or as we come down the stairs; we land on a chair not always softly, but in a manner that hurts (or even affects the chair’s physical integrity). As we see, anticipation is not always successful, or, to use a mathematical description, it is not monotonic. Resilience is reactive: the information prompting the reaction is available in its entirety, or at least to a significant degree. Anticipation is guided by information processes that take place in a context of incomplete information and uncertainty. Its success or failure is indicative of the ability of the living to “fill in” the “missing” data, or to “define” the information, even when such a “definition” is not appropriate, i.e., does not correspond to the context. We fill in missing data more often than we are aware of: crossing the street (no car in view); lifting an object from a hot stove (no thermometer informs how hot the cast-iron pot might be); catching an object we have not seen falling. In some cases, when the reference to reality is lost or disconnected, the anticipation can become delusional: the dynamics of superstition and the associated risk evaluation (e.g., black cats, the number 13, the act of naming someone in order to endow the person with a desired attribute). In a perfectly deterministic world, anticipation is reduced to an evaluation of the difference between the intended and the actual outcome. If risk is defined as the chance that an action will not succeed (in part or in its entirety) and the loss attached to the failed action, then in a deterministic world, there is no risk. This informs us again about the fact that a fully deterministic world does not accept the notion of chance. The dynamics of such a world unfolds in a fully predictable manner. If indeed the deterministic reduction executed by Descartes results in equating all there is to a machine, anticipation within such a system is not possible. The only risk associated with such a description is the breakdown of the deterministic rule(s).

3.1. Taking a chance

The need to examine the relation between risk and anticipation, from the perspective of the outcome of the process considered, should afford us the understanding of the role of chance. Risk involves taking a chance, a concept we anchor within an information-based perspective in which the future is modeled on account of the past. Anticipation, as we shall see, means reducing risk to a minimum. What guides our future actions is just as well an information process in which past, present and future are co-related. Certainly, this first stab at terminological differentiation provides only a preliminary assessment. More should become possible as we take a closer look at how both risk and anticipation inform human activity. For the segment of reality for which our deterministic descriptions are, if not complete, at least adequate, we do not so much need a notion of risk as we need one of that establishes the adequacy of the description, i.e., its context-dependent relevance (for which activity is a given description acceptable).

Indeed, the physical laws of gravity are adequate for all actions that are based on them. A gravity pump will never fail on account of discontinued gravity. (Unlike an electric engine, which depends on the availability of electricity, gravity is permanent.) The gravity pump fails because its components (ducts, valves, pipes, etc.) are subject to wear and tear. Light-based communication (from the lighthouses of the past, with their intricate Fresnel lenses to laser-based links between a space-craft and instruments on Earth) does not fail on account of light’s ceasing to function. Our descriptions of light as the unity of wave and particle might not be perfect, but they indicate that what might affect communication is the failure of the elements involved (the source of light in a lighthouse, the switches between the laser emitter and the receiver, etc.) to perform as defined. The same holds true for many other artifacts conceived around descriptions (such as those of the electron, of protons, of quanti) that make up our scientific understanding of the world. Indeed, in such descriptions – what we call science – we express our understanding of (relative) permanence, and even of causality, which is the ultimate underpinning of risk. The risk that gravity might cease, or that electrons will no longer follow the path described through electrodynamics, or that light might behave other than in the descriptions known as the laws of light propagation, is at best equal to zero.

The interesting thing happens once the human being (as part of the larger reality defining the living) comes into the picture. Indeed, the description of gravity, not unlike the description of anti-gravity, goes back to the observer and makes possible actions guided by the knowledge expressed in such descriptions. Life on a space station, for example, no longer corresponds to the deterministic path implicit in the gravitational description on earth. Other descriptions, of a more complex situation, become apparent not only when objects and astronauts float in space, but also when the cognitive model of the scientists involved, associated with gravity on earth, is challenged by a behavior – their own and that of the objects they use – that contradicts the expected. Suffice it to say that similar observations can be associated with the science expressed in superconductivity, or for experiments with light under circumstances leading to confirmation of light bending in the vicinity of massive bodies (black holes, in particular).

3.2. Classes of risk

The examples mentioned so far have been brought up for a very simple reason: to suggest the relation between what we know and the corresponding notion of risk. There is no risk involved in assuming that objects fall down; there is a lot of risk involved in operating under circumstances where this description can no longer be taken for granted once human activity created new circumstances and unleashed new realities.

Based on these rather sketchy observations, we suggest that risk research can benefit from defining at least three directions:

Class A: Risk associated with the dynamics of the physical world, such as extreme events (volcano eruptions, earthquakes, hurricanes, tornadoes, etc.), but also less drastic changes (soil erosion, excessive load, water infiltration);

Class B: Risk associated with the dynamics of the living (disease, human behavior, interaction);

Class C: Risk associated with the artificial, i.e., the physical synthesized and produced by human beings, such as drugs, orthoscopic devices, buildings, computers, robots, intelligent machines, artificial life artifacts. Such entities are more and more endowed with life-like properties.

The reason for this initial distinction among risk classes is clear: knowledge pertinent to understanding the physical world is fundamentally different from knowledge of the living. And, again, the knowledge synthesized by the living and expressed in the artificial (including artificial intelligence as yet another way to gain knowledge about the world) has a different nature, and a different implicit understanding of risk. The three classes mentioned have an ascending degree of risk. There is an immediate benefit to this attempt to classify risk. We can focus on the knowledge pertinent to the dynamics of the physical world and derive from here methods for assessing the risk associated with it. This is not the same as predicting the event (time and space coordinates), but rather defining its impact in terms of affecting human life and activity. The deterministic knowledge we can derive from our scientific descriptions of the physical world can, in turn, be expressed in operational terms. That means that we can automate processes for risk mitigation in Class A. Several networks of risk-based automated observation stations are actually emerging as we all recognize that while we cannot stop earthquakes or tornados from taking place, we can prepare so as to diminish loss of life and of assets important to people.

There is a relation between the quality of prediction (e.g., how much in advance, how comprehensive the forecast) and the impact of physical phenomena resulting in risk for the human being. An earthquake or tornado affecting a scarcely populated area at a time of a dynamic low (little or no traffic, people away on vacation, etc.) will have an impact different from an event affecting a densely populated area surprised in a dynamic high (heavy traffic, concentrations of people, intense interactions). The prediction and the risk associated with the event – i.e., loss potential – speak in favor of a context-based information system. Class B- and Class C-defined risk are less easy to describe comprehensively, and are not really subject to automation, unless their dynamics and that of the automated system are of the same order of complexity.

As a matter of fact, given the dynamics of the living, we are in the situation that prompted Gödel’s incompleteness theorem [13]; that is, we need to consider to which extent limitations intrinsic to high-complexity entities affect our ability to know them (completely and consistently). Gödel stated that “. . . any effectively generated theory capable of expressing elementary arithmetic cannot be both consistent and complete”. This is, of course, mathematical logic knowledge pertinent to formal systems, i.e., pertinent to our descriptions of reality. If we take only the fundamental thought as a preliminary for examining the living, instead of formal systems for describing it, we realize that completeness and consistency of descriptions of the living cannot be achieved simultaneously. Therefore, to define risk associated to the living – in its particular forms of existence, or in respect to its own actions – implies that we consider partial aspects. For the chosen subset (the risk of slipping on a wet floor, or the risk of developing an infection), we can reach consistency and completeness, but the epistemological price is the same as that prompted by Cartesian reductionism (i.e., local validity).

As far as artificial reality is concerned, we deal not only with the consequences of Gödel’s discovery, but also with the difficulties resulting from generating dynamic systems endowed with self-organization characteristics. The risk that robots and other artificial “creatures” might outperform the human being is better discussed in science fiction than here. But not to address the variety of new interactions between the living and the artificial would mean to ignore new forms of risk and the potential of their rapid propagation in forms we cannot yet account for. We know that we cannot avoid the consequences of the logical principle according to which completeness and consistency exclude each other. But this should not dissuade the attempt to understand interactions even when we do not fully understand the interacting entities.

3.3. The nature of risk assessment

By its nature, risk is relative. Consequently, risk should be approached as a measure of variance in relation to its defining value of reference: a devastating earthquake is risk-free for those who fully insure their property and make sure that their physical integrity will not be affected. (“Away for gambling over the earthquake” could read the ironic note they would leave for those who might knock on their door, if any door remained intact.)

The risk of surviving one’s death is zero. However, the risks associated with cloning are by no means to be ignored. As a measure of variance in relation to a chance outcome, risk pertains to love, procreation, diet, exercise, medical care. While the past is informative regarding variance in the physical realm, when it comes to the living, statistics are, only in a limited way, the premise for evaluating the risk. Finally, in the artificial realm, we might transfer risk experience from the physical (when creating a new material, for example), but we have only limited means for inferring to new circumstances of existence (chip implants, genetically modified seed, interaction with nanoparticles). Even when living characteristics are only imitated, we cannot fully account for their future dynamics.

For the artificial world, the probability description is a place to start from:

risk = probability of breakdown

× losses through breakdown.

A hard disk, completely backed up is, in the final analysis, a small risk, involving breakdown replacement value and associated costs (formatting, time, data transfer, etc.). A hard disk not backed up might cost close to nothing to replace, but the data might be irreplaceable. The risk expressed through the probability of a breakdown is relevant in respect to the possibility that the disk was or was not backed up. The cost of backing up (time, labor, energy, etc.) vs. the assumed risk of facing a disk breakdown is in no relation to the possible loss. Things get more complicated when the process is affected by the variability of the outcome. The implant (heart, liver, cochlea, knee, shoulder, etc.) and the various risk factors it brings up, is of a different order of complexity than the breakdown of a hard disk. And genetically modified seed and genetically engineered products are of yet another scale of risk assessment. Actually, they are all chances we take – in many cases, very daring chances. In other cases, they are somehow less than responsible. (Remember the artificial hearts of the 1970s associated with a nuclear pacemaker, or the idea of having artificial hearts activated through a nuclear battery?) Risk is, it seems, the price we are willing to pay for a certain outcome (winning the lottery, improved health through surgery, landing on the moon).

Without entering into details, we can submit that the three classes of risk so far defined correspond to:

Class A: Risk relevant to deterministic processes characteristic of the physical;

Class B: Risk relevant to non-deterministic processes characteristic of the living;

Class C: Risk relevant to hybrid processes – the artificial is the meeting point of determinism and non-determinism.

The variability of outcome for the risk relevant to the living and the artificial is illustrative of expectations not characteristic of deterministic processes. However, in conceiving the artificial, the human being is dedicated to facilitating a predictive dynamics, even if sometimes this is very difficult. Deeper forms of determinism (in the sense discussed in dynamic systems theory) are engineered, under the assumption – characteristic of Goethe’s Faust model – that we can handle and control them.

4. Is risk nomothetic? Is anticipation idiographic?

There is yet one more aspect pertinent to the classes of risk suggested so far. Wilhelm Windelband, in his inaugural address [34] as Rektor (not really the same thing as president) of the University of Strassburg (when Alsace was part of Germany), brought up the distinction between natural sciences – Naturwissenschaften – and the sciences of the mind – Geisteswissenschaften (traditionally translated as humanities). Research in anticipation and in risk is the object of the inquiry specific to natural sciences, but also to the mind sciences. They provide the description of the dynamics of the physical world, based on which our cognitive elaborations eventually result in defining the notion of risk, along with the means and methods of coping with it. Moreover, it is in the mind sciences that risk is defined as implicit in successful human action. In other words, as we generate opportunities, we generate the associated possibility of failure (total or partial).

The unfortunate distinction between the two types of science proves more resilient than Windelband thought it would be. His suggestion that we’d better look into the “formal character of the sought-after knowledge” remained almost ignored. Windelband observed that the natural sciences seek general laws; mind sciences are focused on the particular. The goal of science is “the general, apodictic pronouncement”; the goal of mind sciences is “singular, assertory sentences”. In effect, we are back at the ancient conflict between the Platonic notion of kind (Gattungsbegriffen) and the Aristotelian individual being (Einzelwesen). They are expressed in sciences of law – the nomothetic, as Windelband called them – and sciences of events – or idiographic. Thus natural science, of law, is contraposed to history, science of events, but only in terms of “the method, not the content of knowledge itself”. Therefore, “same subjects can serve as the object of nomothetic and of idiographic investigation”. Windelband names physiology, geology and astronomy as good examples of the unity between the generality, expressed in laws, and the specific and unique, expressed in the record of change over time. Evolution is his preferred example of how the general law and the individual, irreducible instance need to be understood together. He went on to point out that “the interest of logic has tended far more toward the nomothetic than toward the idiographic”. And he expressed the hope that logical forms pertaining to irreducible single facts or events would emerge as historical inquiry evolved. Laws and forms are the never-to-be disconnected poles. In the first (laws), “thought pushes from the identification of the particular to the grasping of general relationships”; in the second (forms), “the painstaking characterization of the particular”. The tendency towards abstractness vs. the tendency towards making things visible (Anschaulichkeit) defines the “opposition between these two kinds of empirical science”.

But let’s get back to risk by once again quoting Windelband: the cause of an explosion is, according to one meaning – the nomothetic – in the nature of the explosive material, which we express as chemicophysical laws. According to the other meaning – the idiographic – it is a spark, a disturbance or something of the sort. They are not the consequence of each other, and there is no “world formula out of which the particularity of an isolated point in time can be developed. [. . . ] The law and the event remain to exist alongside one another as the final incommensurable forms of our notions about the world”. An airplane flies into a building – law and event. Two airplanes fly into the Twin Towers; three airplanes are supposed to fly into the Twin Towers and the White House; four airplanes to hit the Twin Towers, the White House and the Pentagon. By now we are in a domain where the choreography of the intended event (the design of the terrorist act), the outcome, our ability to effectively anticipate (the event, immediate and long-term consequences, etc.), moreover, the ability to prevent it appear as incommensurable.

Now let us consider the intricate operations of the world markets, the many dependencies resulting from the globalized functioning of the economy, the breakdown of political systems, the global warming scenarios, the oft predicted Internet breakdown, and much more of the same scale. We are confronted with a dynamics that we might attempt to describe in its reductionist-deterministic models – the nomothetic generalizations. But these are also singular events that, after they occur, seem to belong to a sequence in time (history), but do not seem to be the expression of scientific laws. The science behind the events is subject to testing, albeit we have no way to test their historic grounding. Interestingly enough, the deductive mechanism we associate with gaining knowledge from generality (or law) does not guarantee the success of anticipation. Moreover, the incomplete inductive mechanisms associated with particular events along the axis past–present–future are too weak for guiding any effective learning. It is at this juncture that we realize the need for a different perspective altogether if we want to derive practical consequences based on the relation between anticipation and risk.

5. The probability perspective

One dictionary definition of risk is suggestive of what we are going after: the possibility of suffering harm or loss; danger. From the outset, let us clarify the following: although the generality of risk is embodied in the concept – a nomothetic entity – in reality we never face an abstract risk, but rather a specific form. The risk of loss to an insurer is different from the chance of someone’s not paying a debt. The risks involved in traveling (by car, airplane, ship or bicycle) are different in nature from risks pertinent to performance sports. A tenor risks losing his voice or hearing. A bartender risks abuse from bar customers, or robbery after hours; he or she is exposed to the risks of the work schedule. The risk of working towards a useless college degree, the risk of building a home in the wrong location, the risks involved in gardening, cooking or exercising, etc. are all different. We can categorize them, generalize the underlying factors, extract the patterns specific to one or another of those mentioned above; but after the entire nomothetic effort, we will have to concede that risk is as idiographic as anticipation.

After all, none of the sciences addresses risk. The closest we come to associating risk with a nomothetic concept is in examining the relation between risk and uncertainty [18], that is, in trying to extend from the questions of extreme generality characteristic of mathematics and logic to specific forms of human activity. Alternatively, in order to understand how risks are taken, we can look at the sciences of the mind and address questions related to cognitive processes that are related to psychology, ethics, politics, management, social action, cultural theory. The pervasive nature of the subject we call risk makes it very difficult to build what Windelband called a “world formula” – a theory of any and every form of risk. Nevertheless, we can keep records of risk-related events: risks fullyrealized, risks avoided (partially or entirely), wrong risk assumptions, open-ended risks, deterministic risk sequences, non-deterministic risk sequences. In other words, especially under the circumstances of modern data processing (acquisition of information, storage, efficient processing, data mining, modeling, simulation), we can generate accurate risk histories. Such histories are a good source of knowledge about past risk situations. Whether they are of any practical significance for addressing current and future risks, or for the design of new activities in which risk and reward are related, is not so much an open question as it is a matter of realizing that causality – universally accepted – is far more complex than assumed so far.

A relatively similar set of observations can be produced in respect to anticipation. Ante capere, the etymological root of anticipation, points to a preunderstanding, a comprehension of a situation before it occurs. The generality of the notion of anticipation is even more vexing than that of risk. Anticipation is often confused with prediction, forecast and expectation. (The distinction among these terms preoccupied me and I dealt with them in [21].) Let me give one example of a situation in which conceptual discipline could help: “Managed futures trading advisors can take advantage of price trends. They can buy futures position in anticipation of a rising market or sell futures positions if they anticipate a fallingmarket” (cf. www.futures.com). In reality, the action (buying, selling, with the associated risks involved) is not guided by anticipation, but by expectation. The variables on which the price of futures depends include observables (prices, deadlines, etc.) and unobservables, in this case, market volatility. There are ways – based mainly on probability evaluation – to determine the volatility level, but not exactly a calculus of anticipation.

It bears repeating here that all these notions integrate a probabilistic model generated on the basis of statistical data. The past justifies the forecast (certain repetitive patterns serve as a reference, whether the forecast relates to weather, the unemployment rate or fashion trends). The past, together with a well-defined target, defines predictions (regarding health, economic performance, crops). It is the future, in association with the past and the present, that comes to expression in anticipation-guided action: the way we proceed in a world of many variables; the way we perform in sports, in dancing, in resting, in a military campaign; the way we adapt to slow or fast change; the way we risk in order to achieve higher performance. Each anticipation is based on faster-than-real-time modeling, whose return modulates the real-time action. One basic observation needs to be made here: one can risk something (two dollars on lottery tickets), but one cannot anticipate. Anticipation is not a deliberate action. It is an autonomic holistic expression of the living.

In another context [20], I brought forth arguments regarding anticipation as a characteristic of the living. But unlike risk, which is a construct associated with the dangers assumed or inherent in human action, anticipation is what the living, in all its known forms (from elementary to high complexity organisms) carries out in order to cope with change. As opposed to risk, anticipation is not triggered as a definite action or process. Rather, we are in anticipation of danger, opportunity, love, death, the next step, the next position of the body. The possibility that we shall eventually die is one hundred percent; the probability that we shall eventually die is likewise one hundred percent. But the possibility of dying in a certain context (e.g., while sleeping, climbing the Himalayas, picking a flower, during surgery, driving a car, while on vacation) is not the same as the probability attached to the particular context. A “world formula”, that is, an anticipation theory of any and every form of anticipation, would be as good a formula for describing what the living is – probably an epistemological impossibility.

5.1. Probability and statistics

Historic records of events are informative in respect to risk. In respect to anticipation, they are documentaries of a particular anticipation in a given context. Indeed, all we get through the examination of the record of anticipation – successful downhill skiing, return of a tennis serve, fast car racing – is pertinent to a particular information process, never to be identically repeated, so intimately connected to the individuals in action that it is, in the final analysis, an expression of their identity expressed in the action. There is nothing to generalize from this statistical record, no nomothetic form of expression to be expected. The individual in action and the action constitute an irreproducible instantiation of anticipation, one among others.

The risk of falling while downhill skiing is different for the skier and for an insurance company. For the latter, it is well quantified in actuarial tables translating probabilities extracted from statistics and extended to new conditions. These tables inform insurance companies in writing policies that will limit their own risk of loss more than the risks related to an accident. For the skier, falling, while a possibility, never translates into probabilities, but rather into all the anticipatory and reactive actions leading to successful performance – sometimes simply to make it downhill without an accident; other times, to make it in shorter time than the competitors; yet other times, to provide spectacular, high-priced footage without endangering one’s existence. As we know it, possibility theory is an uncertainty theory pertinent to contexts of incomplete information. Probability, in its many expressions, never accounts for a lack of knowledge regarding the past. Randomness supplants ignorance. Each occurrence is viewed as equally plausible because no evidence favors one or another. Probability is based on such (and other) prior assumptions. How likely something will happen (or not) within a defined system is expressed through a quantitative assessment of the outcome. Given a number of n possible outcomes (to win the lottery, to return a tennis serve, to have a tornado hit your house) in a sample space s, the probability of an event x is denoted as P(x) = n(x)/n(s) – that is, how many times event x occurs, i.e., n(x) in relation to all events in the sample space n(s). Very simple rules guide us in dealing with probabilities:

1. The numbers expressing probability are positive and their maximum value is 1.

2. If p is the probability of an occurrence, then 1−p, its complement, is the probability that the event will not take place.

3. For two different events (tornado hitting a house, winning the lottery), the usual set theory rules apply.

5.2. Possibility and probability

Possibility theory makes no prior assumptions of any kind. It encodes quality; therefore it is not a challenging data processing method. It is focused on only two set functions: the possibility measure (Π) and the certainty, or necessity measure (Ν). Early on, as Zadeh [36,37] founded possibility theory, he claimed that an event must be possible before being probable. This is the possibility/probability consistency principle [35].

A probability distribution p and a possibility distribution Π are ascertained to be non-contradictory if and only if (iff) p ∈ P(Π). Despite informational differences between possibility and probability measures, it seems intuitive to select the result of transforming a possibility measure Π into a probability measure p in the set P(Π) and to define the possibility distribution Π obtained from a probability distribution p in such a way that p ∈ P(Π). Let us recall that a possibility measure Π on the set X is characterized by a possibility distribution.

Ï€ :X ? [0, 1] and is defined by
∀A ⊆ X, Π(A) = sup{π(x), x ∈ A}.

On finite sets, the supreme (sup) is a maximum:

∀A ⊆ X, Π(A) = max{π(x), x ∈ A}.

Possibility leads to qualitative inferences: if π(x) > π(x′), we can consider that a certain value of a variable V is more plausibly related to x(V = x) than to x′(V = x′); or, better yet, π is more specific than π! Evidently, for π(x) = 0, x is an impossible value for the variable V to which the possibility π is attached. For π(x) = 1, x is the most plausible value for V.

The possibility of an event x ∈ E, E ⊆ U is denoted by Π(x ∈ E) = supμ min(πx(u)), μ ∈ (u) = supμ ∈ Eπx(μ). Events of possibility 1, πx(u) = 1 for all u ∈ U, are possible, but not necessary. This defines the state of ignorance. Two different possibility distributions π and π′ are one less informative than the other when π′ > π because the set of possible values of the variable V according to π′ (π is included in π′). Having a possibility equal to zero, the event under consideration will not happen.
The necessity of an event x ∈ E is:

in which c is the order-reversing map such that c(p) = 1 − p and EC is the complement of E in U. When it is certain that x ∈ E, we have N(x ∈ E) = 1. To the contrary, if the necessity N = 0, the event is not necessary, but it is not altogether excluded. It is clear that N(x ∈ E) = 0 iff Π(x ∈ EC) = 1 (cf. [25]). The reason for using possibility descriptions is easy to grasp: we want to acknowledge uncertainties while integrating preferences (usually expressed in fuzzy formulations) in the evaluation of risk preferences. At this moment, from a mathematical perspective we have almost all it takes in order to see how transformation from probability (with more information) to possibility measures can be performed. Converse transformations, from possibility (of incomplete, uncertain knowledge) to probability would require additional information, and would result in more than one value.

6. Measurement vs. estimation

The reason for the whole exercise presented above is our suggestion that, between risk and anticipation, there is a structured relation that mirrors the one between probability and possibility measures. The action of measuring is behind probability; the action of estimating lies behind possibility. Both probability and possibility involve objective and subjective components. Given the role that measurement plays in assessing probabilities, and the relation between probability and possibility, it is intriguing here to consider the act of measurement as such. In the physical realm, measurements return values in the R set of real numbers. Goldfarb et al. [14,16] dealt with the many implications of this foundation in his new ETS (evolving transformational system) model.We shall return to this as the analysis makes clear that we need an alternative framework for understanding the relation between risk and anticipation.

We know quite a bit about inverse problems: they are a particular type of description of physical systems. The observed data – pertinent to, let’s say, astronomy, geophysics, oceanography, or human-made physical artifacts (the artificial world, cf. Class C risk), the functioning of a bridge, the operation of a computer, the performance of a chair over time – can guide us in finding out the still unknown parameters of phenomena within the domains mentioned above or of similar entities. Obviously, some of them are more complex than others, which means that some are more difficult to measure than others. In addition, the integrity of the observed data is not necessarily guaranteed. It is definitely easier to observe the functioning of a chair, and even of a bridge, than to quantify astronomic phenomena or geophysical systems. Noise plays an important role, too; so does the linkage among measured parameters. Provided that linkage is obvious or already established, we can handle it. But many times, correlations of all kinds run the gamut from the subtle and still discernible to the more subtle and almost impossible to distinguish. (We shall return to the notion of linkage shortly.)

All our observations and measurements involve means and methods for performing them. Therefore, in addition to noise, measuring procedures affect the system under observation. And, as we’ve already noticed, to make things even more difficult, observations are not always independent of each other. The major assumption presented so far is that the dynamics of physical entities is expressed in a nomothetic description, i.e., law. Newtonian gravity or fluid dynamics, or thermodynamics are such laws. They guide us in the modeling effort – how the bridge behaves; what the model describing a black hole in astronomy is; how a tsunami starts. Some models are further used for simulations: a computer falling; the numerical simulation of the 1992 Flores tsunami; simulation of fluid dynamics. Associated with observations over time (idiographic aspects), the models are continuously refined. This is known as the fitting of data effort.

6.1. An example: Global warming and the associated risks

In our days, one of the most prominent examples of reverse modeling is expressed in the predictions of global warming. The observed data has hardly been questioned. The unknown parameters, which cannot be measured directly, are fitted to the model. The inference that, in addition to known factors affecting the meteorological condition, human-based patterns of behavior resulting in high carbon dioxide emissions affect global warming is the result of an inverse problem resolution (far from meeting unanimous endorsement in the world of science). This example illustrates the difficulties associated with the inverse modeling approach. If we consider the associated risks, i.e., the variety of risks related to global warming, we easily realize that the degree of mathematical confidence in inverse modeling is reflected in the confidence of risk management methods. The evaluation of probabilities, associated with physical processes to the estimates of risks corresponding to such probabilities, propagates uncertainty. Global warming, in respect to which many risk aspects end up as headlines in the mass media or become the subject of political controversy, is a good example of an inverse problem approach (and of its inherent limitations). We shall not take sides in the heated debate – although risk research should always be prepared to debunk end-of-humankind scare tactics. The example is strictly illustrative.

Central to the scenario of the dangers that global warming entails is the role played by “greenhouse” gas emissions. The model was conceived over a long time, and there is a lot of data that can be used to describe the short-term behavior of the system. For the long term, the mathematics of the inverse problem comes in quite handy. Those who practice it examine the responsiveness of the energy markets to economic controls made necessary by international agreements with the goal of reducing greenhouse gases. Since the forward problem is not even well defined, scientists proceed with generating data that is supposed to drive the model in such a way as to fit the current situation. Given the nonlinearity of phenomena in the knowledge domain to which global warming is but one of many components, it is easy to understand why some scientists predict the melting of arctic icebergs, and others, a possible ice age, each capable of triggering a cascade of increased risk events. The intricate nature of the scientific arguments should not affect the awareness to ecological aspects that was prompted by researchers who applied inverse problem methodology to confirm predictions of global warming originating from outside scientific discourse. A variety of statistics, regarding land use, afforestation, etc., provide yet other data for the inverse problem.

6.2. Risk and monotonicity; anticipation

Any fact derived from the examined aspect may be extended, provided that additional assumptions are made. If our description of a risk-entailing action is modified along the line of adding new conditions, the new description remains valid. Paying for a lottery ticket using one’s own dollar bill, or a borrowed dollar bill, or four quarters is equally risky. (The act of borrowing adds risk, but not to the act of buying a lottery ticket.) The outcome-based understanding of risk and the understanding of anticipation as expressed in successful action make us aware of the fact that Class B (i.e., concerning the living) risk mitigation involves anticipation as a decisive factor. The tsunami of December 2004 was indicative of how certain segments of the living system coped with the fatal danger by proactively avoiding it: animals sought refuge at higher elevations. That some people actually went to the deserted beaches, now enlarged through ocean retraction, and played soccer in that eerie atmosphere preceding the wall of water that crushed them is an eloquent example of anticipation that failed due to the denaturalization peculiar to societies that found their new “nature” in the artificial world. As an autonomic function, anticipation is not automatically successful; that is, monotonicity cannot be taken for granted. Therefore, risk assessment and automation need to compensate for the possibility of anticipatory failure. The sensor network, which is part of the tsunami alert system, was completed and improved shortly after the disaster. It added to the artificial environment yet another network of sensors and data analysis tools that effectively replaces the natural.

Unless an agent (person or program) examines the observations from the perspective of assessing the monotonicity of a system’s dynamics, there is no reason to introduce the notion of risk. Only when, for some reason implicit in the system, or external to it, monotonicity is interpreted as prejudiced – for example, the last time the ocean earthquake did not result in a tsunami – do we have a risk perspective.

Each interpretive agent has to be able to distinguish between information independent of the observations, called a priori information; and a posteriori, i.e., resulting from inferences we make from the observations and the a priori information. Since nearly all data is subject to some uncertainty, our inferences will always be in some ways statistical. Three fundamental questions will have to be addressed:

1. The data is less than accurate: Do we know the consequence of this condition of data when we fit the data?

2. Since the model used and the system’s response are related, how good is the model?

3. What do we know about the system independent of the data? In other words, do we know how to find the models that might fit the data but are actually unreasonable?

This last question is important since every inverse operation returns many models from among which only some are acceptable.

As already pointed out, the science of global warming has already returned a variety of models that are neither a complete description of what might happen nor a consistent description. And since we do not have effective ways to discern between the acceptable (not for public consumption or political purposes) and the arbitrary, we shall continue to work, in this and other areas of concern, guided by intuition rather than by analytical rigor.

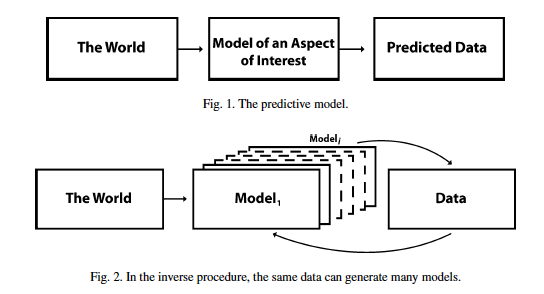
In a more systematic analysis, we face, initially, the forward problem: define a model, i.e., an embodied
theory that predicts the results of observations (cf. Fig. 1). It all looks relatively simple: a reductionist progression from the complexity of what we call reality to the lower complexity of high-level causal description of a certain aspect of reality (e.g., gravity), to data collected from an experiment, for example: dropping equivalent quantities of feathers, water, and metal from the same height and determining how long it takes for each to reach the level zero of reference. Intuition, for example, would have said that the feathers will take longest.

The degrees of freedom of the variables in the world are higher than the degree of freedom of the variables in the model. Still, even for the simplest aspects of reality, and even assuming a continuous function of the space variables, it is difficult to imagine how one would proceed from the finite space of the data (corresponding to a finite number of measurements) to a model of space variables with infinitely many degrees of freedom (cf. Fig. 2).

The fact that from the same data many models can be generated – that is, we face the problem of lack of uniqueness – is further compounded by the noise implicit in the observations (i.e., measurements). Assuming that somehow we can choose from among the models that result through the inverse procedure, given the non-linearity of the procedure, data fitting is, evidently, non-trivial. But these considerations, relevant more for drawing our attention to the difficulties inherent in the procedure, are of relevance to evaluating risk as it pertains to the limited aspect of the world – the physical and the artificial. If, however, pursuing the path of distinguishing risk associated with the living as different from risk limited to the physical world (again, earthquakes, tsunamis, volcano eruptions, hurricanes, floods, etc.), we soon realize that we need to account for the specific ways in which information processes affect the dynamics of the living. Indeed, in the physical realm, the flux of information corresponds to the descriptions of thermodynamic principles.

6.3. A model of models

The living, while fully subject to the laws of physics, receives information, but also generates information [20, p. 101]. In dealing with the relevance of the Second Law of Thermodynamics for biology, Walter Elsasser [6] remarked: “Every piece of evidence to the effect that inheritance of acquired properties does not exist makes it harder to understand why deterioration of genetic material according to Shannon’s law is not observed” [6, p. 138]. He concluded: “It becomes indispensable to introduce the observed stability of organic form and function, over many millions of years in some cases, as a basic postulate of biology, so powerful that it can override other theoretical requirements” [6, p. 139].

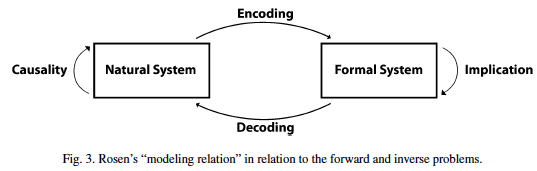
Rosen [27,28] tried to avoid the quandary of the problems we face as we consider the inverse procedure. He advanced the modelling relation (Fig. 3). It is clear that our focus on the inverse function pertains to the Formal System, i.e., the encoding of knowledge about the natural system in some formalism (mathematical, logical, structural, etc.). Encoding is, for all practical reasons, the forward function: observe the natural system and describe it. Descriptions are representations: they stand for the represented. Such descriptions are symbolic expressions (i.e., conventional in nature). After they are processed in the Formal System, we can proceed with the inverse, here defined as decoding. It means: if we change something in the representation, how will such a change be reflected in the present? Genetic engineering, with its risk space, is the best example of this. By design we change elements of the genetic code and see how such changes affect the real object – the cell, the organ, the organism, the species. The risk involved in the inverse operation is rarely fully understood. What needs to be clarified here is that anticipation is intrinsic to the natural system (the “real thing”) and, in Rosen’s view, takes the form of entailment. The risk aspect is evidently connected with the Formal System and returns, through decoding, information related to the outcome of the dynamics of

the natural system. In addressing the processes through which the living observes the world and itself, Fischler and Firschein state: “. . . the senses can only provide a subset of the needed information; the organism must correct the measured values and guess at the needed missing ones” [9, p. 233].

With the understanding made possible by Rosen’s model and the realization that the living takes an active role in processing data – corrects some of it, guesses what is missing, drops the less relevant – we realize that in every inverse procedure we need to introduce estimation procedures. Indeed, guesses at missing data are estimations, and so are corrections of data (sometimes data is “cleaned”, i.e., made noise-free, or uncertainties are lifted) or omissions. No estimation is unique; usually there are quite a few acceptable models that correspond to a data set. Moreover, even when the forward problem, from the physical system to its formal description, is linear – and this is the case most of the time – estimations leading to an approximate model may be non-linear. In the domain of the living, linearity is almost the exception. Experience in advancing estimated models shows that the expectation – what it means to be an acceptable model – affects the procedure. Between the model and the estimated (approximated) model lie differences expressed in terms of errors. Some are deterministic; the majority, corresponding to uncertainty, is statistical. All this has direct consequences for our attempt to define the risk implicit in the majority of our endeavors. Among the few available conceptual tools we can utilize are those developed within fuzzy logic and the Bayesian probability theory. This theory describes the degree of belief (or credence) upon which probabilities (of events, risks, etc.) are defined. It stands in contrast to frequency (or statistical) probability derived from observed events.

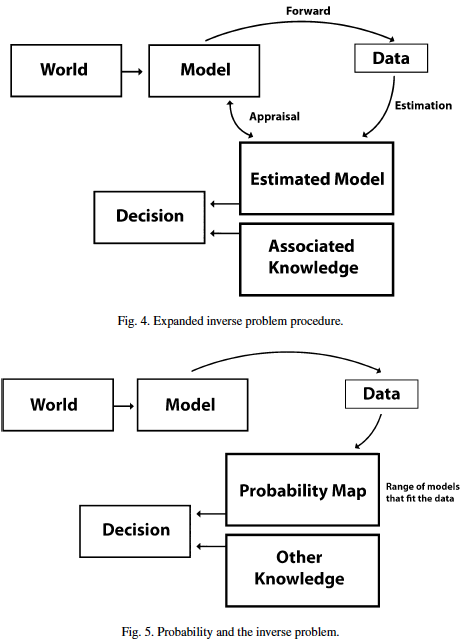
Since inverse problems are solved for practical purposes (pragmatic condition), the estimation is guided by the activity’s outcome. A physician examining a patient proceeds along an inversion: blood test values as a basis for a diagnosis. The geologist proceeds from seismic data to the decision whether it makes sense to drill (Is there an oil reserve? How big? How deep? How difficult to access?). The investment advisor might use a model derived from an inversion of financial data (Where would you like to be in 20 years from a financial viewpoint?) as a basis for formulating a customized strategy. As it becomes evident, the estimated model (for a medical diagnosis, for geological assessment, for investing) is associated with other data reflecting the professional’s expertise and the context for the risk decision. Uncertainty shadows the process. In the final analysis, the outcome of the process is not the inverse function, but rather the pragmatic condition. Since we are what we do, the outcome is predicated by the actions guided by the inverse function assessment: The doctor will recommend a change of diet and will define the risks resulting from not observing it. The geologist will argue in favor of more exploratory data, or for a pilot exploration before investing in a large operation. The geologist will quantify the risk for each procedure suggested, against an alternative course of action. The investment advisor will spell out means and methods for increasing a person’s wealth, while defining the variety of risks faced as world markets experience their periodical ups and downs.

The diagram (Fig. 4) makes clear that data is subject to error and uncertainty. The arrow from the data, including the arrow relating the estimated model to the variety of models generated, is the conduit for error propagation. Probability descriptions (of data) affect the entire inverse process (Fig. 5). However, the decision is based on explicit or implicit risk assessment (What will the outcome be?) rather than on probability (What are the chances of being wrong?). The risk of misdiagnosis is mitigated by the nature of the process: more data can be generated, better estimates can be made, the approach can involve alternative interpretations. The economic risk associated with the decision to drill, together with the associated environmental risk, makes it clear that the probability (of loss or profit) is part of the decision process. Models are uncertain; decision-making compensates for uncertainty. In the investment model, probability extends to

a changing context, i.e., to a very complex mapping from the present to evolving probabilities. Estimation plays a huge role, and it is unclear whether in such a case (as in many others) it is advisable to work on an estimated model or on defining the model’s characteristics, that is, a range consistent with the data.

There is a definite difference between the estimation and the inference paths. In the estimated model, frequencies count (as in defining information based on a coin toss), informed by the distribution of trials (best example, playing the lottery). In the inference model, it is not the repeated outcome of random trial, but the information (or lack of it) that informs our expectations: “20% chances of rain” means different things in different places (compare weather prediction in Northeast Texas to weather prediction in England, France or Germany). In the end, it means that we have a prior probability model that we combine with observed meteorological aspects (wind, clouds, barometer, etc.). It is not at all clear that more data (from more stations), or more and better data (acquired with improved instruments) can lead to better predictions (in the sense of improved understanding of causality). The prior probability, i.e., the deterministic inference path, is no less relevant than the data, but much more difficult to improve upon.

6.4. Prior knowledge (subjective or objective)

As a matter of fact, the newly observed parameters influence the prior information so that a conditional model (based on observed conditions) results. Nevertheless, the method simply says that our perception is influenced by prior knowledge, subjective or objective: “If I hadn’t considered it (intuition, belief, guess), I would not have seen it”. Many pragmatic instances are the result of not considering what, after the action, proves more significant than usually assumed. Risks are often taken not in defense of data, but rather because the weight attached to some aspect of it is way off in respect to its significance. Correcting data, guessing [9] takes place in this context. Prior information, i.e., probabilities, is related to prior experience, to mental and emotional states, prejudices, or biases – experience, in one word. If the reverse function sought implies some practical activity (such as panning for gold, searching for diamonds in areas known to contain them), one can perform an empirical probability analysis in a sequence proceeding from initial data (e.g., how much dirt or sediment can one process in preliminary panning?) to the next steps (such as “found a diamond”), while the final outcome remains open. The metaphor of “tunnel vision” describes the risks involved in pursuing prior knowledge or discarding it.

The estimation path and the inference path (usually involving Bayesian probabilities) are better pursued in parallel. What is essential and unavoidable is that in any inverse problem attempt, one begins by realizing what the uncertainties are in the data to be considered. Specifying prior information is what distinguishes the individual approach. Together with the choice of the model, this constitutes the art of inverse problem solving. Indeed, it is an art; it is an idiographic operation with no guaranteed outcome, and therefore, a risky operation. Geophysicists examining the surface of the planet with the hope of thus gaining knowledge about what lies beneath pushed the understanding of the inverse problem into the public domain. Some of them [31] noticed that the data recorded by seismometers located on a volcano’s slopes and the data predicted by volcano models are “hopelessly different”. Moreover, they also had problems with the non-uniqueness of the path from data to a model: “there are infinitely many possible models of mass density inside a planet that can exactly fit any number of observations of the gravity field outside or at the surface of the planet” [31, p. 493]. The non-uniqueness of the path from data to the model explains the large variety of hypotheses entertained by those involved in the inverse problem approach. Imagine a work of art: painting, symphony, architectural work. And think about tracing it back to the rich multi-dimensional matrix of all factors involved in its making. There is no unique, backtraceable, reverse engineering way to get to the initial circumstances and to the many choices, some possibilistic in nature, some probabilistic, some deterministic and some non-deterministic, that were made as the work emerged.

Imagine now that the subject of the inverse problem is nothing other than a living entity, in particular the human being. The reason for even formulating the problem is at hand: if anticipation is expressed in action, what are the risks associated with human actions? Moreover, can we fit the data pertinent to an individual to the model characterizing anticipatory expression?

7. The anticipatory profile

Can we measure or otherwise describe anticipation? Can we measure or otherwise describe risk? We have argued at length (cf. [20], and in this article) for the simultaneous consideration of probabilities and possibilities associated with an event. In this final part of the paper, the focus will be more on various aspects of measurements, as a necessary step towards the realization of a different form of mathematics for eventually describing anticipation. The entire endeavor is informed by intensive research that involved human subjects evaluated in a setting propitious to the expression of anticipation and to its partial quantification.

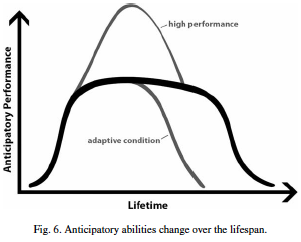
But before we describe the measurement procedure, here are some preliminary considerations. First and foremost: Anticipation is a holistic expression of theorganism as part of a dynamic environment. The holistic begs explanation. For reasons of brevity, we will adopt here Elsasser’s careful ascertainment: “. . . an organism is a source (. . . ) of causal chains which cannot be traced beyond a terminal point because they are lost in the unfathomable complexity of the organism” ([6], p. 37). Therefore, no reductionist approach can help defining the many interwoven processes, from the molecular level to the entirety of the organism in the environment. Interaction with the environment eventually results in anticipatory action. Anticipation is a necessary condition of the living. Second: Anticipation is an autonomic function of the living. Third: The dynamics of the living organism is reflected in the change over time of its anticipatory characteristics. Newly formed organisms acquire anticipation; each individual organism has its own anticipation-related performance within the evolutionary cycle; aging entails decreased anticipation; death returns the organism to the physical reality of its embodiment (Fig. 6).

For more details on anticipation, the reader is encouraged to read Rosen (Life Itself: A Comprehensive Inquiry into The Nature, Origin, and Fabrication Of Life and Essays on Life Itself ) and Nadin (Mind – Anticipation and Chaos and Anticipation – The End Is Where We Start From).

Against the background of the attempt to quantify the change in anticipatory characteristics in the aging, I revisited some of the examples accumulated in the rather modest literature that acknowledges anticipation as a research subject. Early on, Gahery [10] was intrigued by Leonardo da Vinci’s sentence: “. . . when a man stands motionless upon his feet, if he extends his arm in front of his chest, he must move backwards a natural weight equal to that both natural and accidental which he moves towards the front”. Leonardo made this observation by 1498 (Trattato della Pittura), prompted by his study of motoric aspects of human behavior. Five hundred years later, biologists and biophysicists addressing postural adjustment (Gahery cites Belenkii, Gurfinkel, Paltzer, 1967) proved that the compensation that Leonardo noticed – the muscles from the gluteus to the soleus tighten as a person raises his arm – slightly precedes the beginning of the arm’s motion. In short, the compensation occurred in anticipation of the action.

After learning about Leonardo’s observation, at the seminar on Anticipation and Motoric Activity – A Meeting of Experts (December 2003, Delmenhorst, Germany), I contacted Gahery and we exchanged some ideas concerning preliminary actions in a variety of motoric activities (gait initiation, posture). Since those days, I have considered ways to translate Leonardo’s qualitative observation of more than 500 years ago into some quantitative description. Gahery observed that quite a number of human actions involve preparatory sequences. But he did not measure either the timing of such actions or their specific cognitive and motoric components. Let us examine Leonardo’s example (Fig. 7). This representation can inform a model – from the mental representation of the action to the sequence of muscular activity depicted in the diagram – and finally to the lifting of the arms. The challenge is to create a record of events, some following a sequence, others taking place simultaneously (parallel processes).

At the current state of technology, researchers cannot obtain detailed information on the brain activity of a subject in action. We know that damage to the human prefrontal cortex (cf. The Iowa Gambling Task [2]) can result in insensitivity to future consequences. But it is not possible to check this in a situation where one can drop a ball without realizing what that entails. The best we can do is to consider EKG sensors applied to the skull. As of the day of this writing, such sensors, integrated in a skull cap, serve as an interface to a new category of games driven by the “thinking” of the persons playing those games [5]. The author refers to the companies Emotiv (USA/Australia) and Guger Technologies (Germany). The sensors can, in principle, “read our minds”. (The science of this skill is still quite preliminary, even though experiments started well over ten years ago.) But they cannot show us how the brain works. We can, however, monitor muscle activity. In this sense, EMG sensors can be placed in such a way as to inform us about particular muscle group activity (time information, intensity of muscle engagement). Finally, we can integrate such information with the precise description of movements resulting from motion capture. This is now a relatively mature technology that provides a high-resolution representation of human movement, plus the data associated with the movement. The matrix representation of body movement corresponds to an integrated description from singular points (corresponding to the joints and to other parts characteristic of the body in action) to the continuum of movement. If we synchronize it with the sensor information, we can know exactly when raising the arms is preceded by tightening of the back leg muscles. With all this in mind, we have a situation in which we can carry out the forward function – deriving data from the model – and inverse function – generate, from the data, the model that fits the action, i.e., figure out the sequence of cognitive and motor activities that allow the person to maintain his or her balance. Even a situation as simple as the one described above ends up challenging currently available computation resources, and even more our ability to integrate data streams of various time scales. Given the complexity of the situation,

we have so far implemented the integration of motion capture and EMG sensor information (Fig. 8).

From the experiments carried out so far, we have
been able to gather synchronized data (Fig. 9).

7.1. Examples (Class B and Class C risk)

While this is not the place to go into more details regarding the expression of anticipation, we need to connect the dots to risk analysis. We will first suggest a Class C risk, concerning the artificial, i.e., a humanmade artifact with endowed dynamic characteristics that emulate the living; and Class B, concerning the living. If instead of an organism we had a crane – an artificial construct designed for the purpose of lifting heavy materials on construction sites or in other contexts – we could proceed in the classic manner. First we would define the exposure: in other words, the known parameters at which the machine functions (spelled out in detail in the technical documentation) and the uncertainty associated with operating the crane (correct identification of every object through its weight, the margin of error, the factors that might affect the operation, etc.). The risk associated with the “breakdown” of the “machine” – lost stability, breakdown of a part, cable, trolley, errors in operating the crane, etc. – can be easily calculated on account of the additive properties of probability expression.

A crane, no matter what type, is based on what is called mechanical advantage: using the principle of the lever, a heavy load attached to the shorter end is lifted as a smaller force, applied in the opposite direction, is applied to the longer end. The pulley affords the mechanical advantage as the free end is pulled (by hand or through some machine) and the load, attached to the other end, is moved by a force equal to that applied,

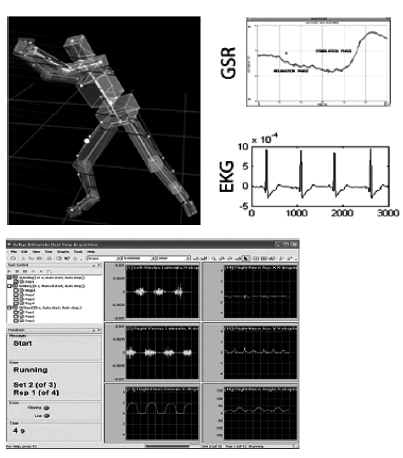
Fig. 9. Motion capture integrated with sensors yields synchronized data.

multiplied by the number of lengths of cable passing between the fixed block attached to the weight. Every crane is defined by the maximum weight it can lift under the assumption of stability. To achieve stability, the sum of all moments about any point, such as the crane’s base, must be zero. In order to reduce risk, cranes operate at a fraction (75–85%) of the maximum load. Tower cranes, truck-mounted cranes, crawler cranes, gantry cranes, and a variety of others conceived, produced, operated, and maintained according to their respective risk maps (e.g., structural failure, collapse, contact or collision with other structures, falling objects). Procedures for lowering the risk associated with crane operations (inspection, tests, required maintenance, repair specifications, training, etc.) are possibilistic maps of what can go wrong. Probabilistic considerations translate into norms regarding crane production and operation, as well as maintenance requirements.

The risk associated with human beings’ lifting their arms is zero for most of our lives. Short of having rotator cuff problems or some other shoulder condition that can be aggravated by lifting the arms, the movement poses no risk. But as humans age, stability becomes questionable; thus, older subjects avoid movements that can result in instability (and eventual falling). Others, afflicted with arthritis or spurs, will not risk more pain.

We are now specifically at the intersection of the space of possibilities – what a person can perform – and of probabilities – what consequences there might be. Beyond this example of quantifying anticipation, we have the possibility to further collect all kinds of data related to human action. Such data pertains to how we breathe, to heart activity, to galvanic response, to tympanic temperature (informing us about brain involvement in certain actions). Indeed, if anticipation is a holistic expression, we want to capture as many details of the whole as possible. Let us consider such a description, still partial, and let us discuss some aspects of the potential data.

Sensors translate functional properties at the physiological level into signals.We understand measurement, in its most general definition, as an interaction between what is measured (quantifiable) and what we use for measuring, i.e., a quantifier (e.g., a stick, a counterweight, light reflection, electric measurement device, etc.). As such, sensors are quantifiers. The dynamics of interest to us – that of the whole body in its very high complexity – is sampled via sensors. The dynamics induced into these sensors from the observed biological elements (skin characteristics, saliva, temperature, etc.) is expressed through entities, such as signals (and their characteristics – amplitude, frequency, etc.) and states. That each biological component functions at a different time-scale (has its own clock, in other words) makes the issue of integrating sequences of information pertinent to dynamics extremely difficult. Just for the sake of illustrating the breadth of the time-scale (important for the bandwidth of the channels used for integration), let us notice that we are covering a dynamics extending from milliseconds to minutes and hours (Fig. 10).

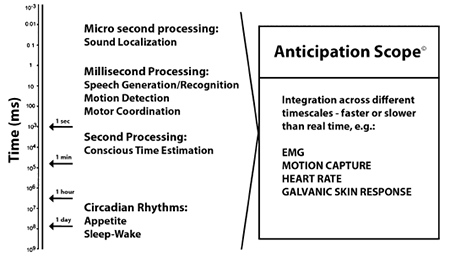
Fig. 10. Time-scale in the human being.

Given the various biological rhythms – at the genetic, molecular, neuronal, organ levels – one aspect begs our immediate attention: synchronization. The models of a centralized mechanism for synchronization (“the conductor” in the “concert” we call living) or of distributed, interlaced processes, come up as hypotheses to be pursued as we gain better knowledge of how anticipation is expressed and risk is assumed. After all, the functioning of the whole we call organism and the holistic expression we identify as anticipation are themselves not risk free. The possibility that something might go wrong (not perform as expected or break down) was translated over long evolution cycles into many embedded redundancies. Therefore, the risk of having no anticipation expression or the wrong anticipation is low, but by no means zero. Given the fact that anticipatory processes are ultimately nondeterministic, we could define risk as non-successful anticipation (of not returning a fast tennis serve, of losing balance, of not realizing the center of gravity, as in Parkinson’s disease). In other words, anticipation translates into successful adaptive performance. Risk pertains to all that might make it unsuccessful. This systemic definition of risk, as applied to Class B risk (the living), can be further generalized. What for an engineer working on the crane problem appears as:

risk = probability of an accident

× loss per accident

for the organism would be

risk = possibility of an unsuccessful anticipation

× consequences of unsuccessful action.

But, as opposed to the functioning of an airplane, the launching of a rocket or satellite, the meltdown of a nuclear power plant, the organism has a memory, can learn and adapts. Artificial entities currently produced are conceived and built with memory and can partially learn and even adapt (albeit to a limited number of situations). This makes the focus on Class B risk even more important. Therefore, consequences are to be seen within the broad evolution cycles, rather than exclusively related to the particular organism or to a particular “life-like” artifact.We also better understand why, in generating an artificial reality, human beings project, as much as possible, from their own characteristics onto the new artifacts they design and produce. Within the same evolutionary cycle, it becomes clear that the living is, across species, risk seeking. It is in this function that anticipation appears as the underlying informational process that pushes towards higher performance at the peril of circumstantial or even systematic risk-taking. At a certain level of the living, there is the explicit awareness of risk-taking, along with the related psychology of regret when risk was not assumed, or when risk-taking returned less than the anticipated outcome. In his Commentary, Albert Tarantola, the Sorbonne geophysicist, referring to what he calls the “Darwinian adaptation of animals” notes: [animals] “do not spend too much time understanding the uncertainties; one model of the world must be adopted (a predator is approaching) and adequate action must be taken (Run!)” [31, p. 493]. But when this survival pressure does not exist, we can consider computing the maximum of imaginable models (computation is getting cheaper by the day). After that, we compare empirical observations to our predictions. Since uncertainty in observations (quantification) as well as in the theory guiding us in modeling cannot be excluded, we need to account for the consequences. The result is a smaller set, which can effectively guide us in understanding how the delicate balance between anticipation and risk is maintained in the dynamics of the living.

7.2. Model and quantifiables

The AnticipationScope™ is a quantifying platform that ultimately can help us characterize how anticipation and risk are correlated. To understand the correlation process, let us take a closer look at the intricate nature of our measurements. To quantify is, after all, to extract, i.e., to mine, a characteristic or several, based on which nomothetic and idiographic aspects of an organism can be described. Given the complexity of the living, it is obvious that there is no unique quantifier. As a matter of fact, in daily life many measuring units, some more adequate than others (in respect to a certain context), are deployed. Our goal is to advance a coherent and consistent quantification method. This consists of a model and of quantifiables (Fig. 11).

The complex organism called the individual is part of the broader real world. This belongingness is embodied at many levels – metabolism, self-repair, interaction. Fundamentally, at the pragmatic level – besides all other labels (name, gender, blood type, race, age, social role, etc.), individuals are what they do. In the AnticipationScope, they can perform a large variety of physical and mental tasks. They can also interact. Given the above-mentioned statement that anticipation is expressed in action, and that risk is the possibility that an action might go wrong – the action can be jumping, or initiating a stock market transaction, catching a ball or misinterpreting a cue – the Anticipation- Scope quantifies action in terms pertinent to a description of physical movement; quantification of cognitive processes; and quantification of associated motoric activity.

7.2.1. Model, quantifiables, states, intervals

The model is that of an organism receiving sensorial information, but also generating information. The model also ascertains its open nature, as well as the interconnection of many processes, each taking place on its own time-scale, though not even necessarily a uniform scale. The state of the organism is described within the quantification convention adopted: it can be that a quantum description more than a discrete representation will eventually be more adequate even if not necessarily easier to handle.

The quantifiables, i.e., features we want to characterize, are also mapped from the AnticipationScope to numbers or quantum representations. It should be clear that the state of an organism at any moment in time t, denoted as state of an organism X at t, S(X)ti = si, for short, q(si), will be represented by S (S(X)t), i.e., state of the quantifier as induced by State(X)t of the quantified at time t.

State means nothing else but what the organism is doing at a particular instant in time. The quantifiables are no more than a mapping from states of the organism to states of the quantifier (in particular, sensors). These, in turn, can be discrete number representations or quantum descriptions (such as “it is in state A¯ and non-A”). The specification of a quantifiable on a state S(X)t takes place through sensors. Each sensor has a predefined reference. If q(si), the state of the quantifier corresponding to the state si of the quantified depends only upon si, we have the premise for a forward function that will return meaningful values for our interpretation. If the correspondence is influenced by factors other than si, inferences from q(si) to si become problematic. The entire quantification sequence describes a functional mapping f: set of states {si} ? R, either to numbers in the set R, or to possible structural representations, or to quanti. We mention here all of these possible descriptions, from which only one is usually performed. The functional mapping is the pointing to classes: Class A, Class B, Class C. Every quantifier – again, only one description is usually performed, such as sensors, in our case – defines an observable; reciprocally, we assume that for equally quantifiable aspects of the organism, there exists a sensor in whose specific output it can be described.
All this leads to a statement of principle: the living is the unity between a physical substratum (subject to the laws of physics) and associated anticipatory characteristics. This being the case, we can quantify descriptions of the living as the unity of its physicality and its own dynamics of anticipation, as subsets of the whole making up the organism. This procedure is actually the consequence of the generalized principle of complementarity already introduced in this paper. Moreover: while the physical accepts synchronic descriptions – sections (or “photographs”) at a given time of measurement – the living can be meaningfully described only by considering intervals, the diachronic record (the “film” of life):

observed interval ti ? tj

⊇ history of the organism, diachronic record.

If a quantifiable affects the organism’s functioning over its entire history (from birth to death), such a quantifiable is identified as essential. If a quantifiable affects the functioning of the organism over some intervals – during a certain defined action, or during a specific life function such as giving birth, or during free fall – it is called significant. If a quantifiable does not affect the functioning of the organism, it is called non-significant. A person’s hair color is probably nonsignificant in respect to physical performance. However, it is difficult to give examples of non-significant quantifiables, because everything that is part of the holistic entity we call an organism affects and is affected by its functioning.

We can generate a map of quantifiables related to living events (actions) and attach weights to them (from 0 for non-significant, to 1 for significant) and establish a precise action sequence. Some quantifiables can be discounted due to their low significance. In some ways, that would mean to anticipate as we quantify. Since the description of an organism impliesmultiple observables, we would have to address the many aspects of deploying a large variety of sensors and of integrating their output in the synthetic representation called the Anticipatory Profile (Fig. 12):

In other words, the functions f₁, f₂, f₃, . . . , f_i describe observables over a state si in the organism in independent ways: f₁(s_i), f₂(s_i), . . . , f_i(s_i). In view of this, we have to address questions such as:
1. Are the quantifiables independent of each other?
2. Are there any links to be expected or established after the quantification?
3. Can we establish relations among the quantifiables (one-to-one, one-to-some subset, between two subsets, among several subsets)?
The space defining the state si is multidimensional. The coordinates f₁(s_i), f₂(s_i), . . . , f_i(s_i) are said to be unlinked when and only when
(a) the numeric representation R_f, or
(b) the structural representation, or
(c) the quantum representation
are independent. Each descriptor R(f₁), R(f₂), etc.
mines a different aspect, let’s say a numeric description of the state (s_i). The level of distinction between such descriptions can itself be quantified. However, in some cases there are links – some that we identify as a priori knowledge; others that might constitute postexperience knowledge. We can consider the possibility that R(f₁), R(f₂), etc. are linked, or the probability that they are linked. In any case, when such a link between two quantifiers is established, one becomes a function of the other.
Interestingly enough, many times our approach to the living is to accept the intrinsic linkage, even if such a linkage is weak – think about how blood tests are linked to a variety of conditions, from infections to early references to cancer cells – or very discrete. The reason for accepting a larger state space – and thus the challenge of processing the data – is very simple: linkage is a good means for some limited prediction. Indeed, if f₁ and f₂ (for example) are linked within the state we are trying to describe, then we can mine information about f₂ by determining f₁ (a particular case of the inverse problem). This reveals that linked quantifiables do not have to be “sensed” individually. We could, in principle, compute them if the nature of the link is known, and the relation translates into a computable function. After all, to quantify means to deal with the result of the interaction between the organism subject to quantification and the sensors (defined as quantifiers). When the information from the sensors proves to be linked, we can substitute the process of measurement with one of computation. Richard Feynman, famous for his deep understanding of computation [7,8], would probably have claimed that quantum computation would be the adequate processing. Inspired by him, I claim that actually, anticipatory computation would be the only form acceptable for quantifying processes that accept, together with the deterministic sequential model of the von Neumann machine, the vector of time from the future to the present.
An anticipatory computation, expressed as living computation, is characterized by the fact that each of its successive current states depends on a previous state, the current state and possible future states. In addition, an anticipatory computation is reversible.⁴ The suggestion we make henceforth is to complete the family of known forms of living computation (Fig. 13).

The six families of bio-computing have some similarities, but also fundamental differences. If we are trying to answer the question that guides the effort of quantifying anticipation – how do quantifiables relate to a change in the state of the organism? – we soon realize that for a number of the variables considered, we obtain a good image of the deterministic processes involved in anticipation. For others, we end up with an acceptable characterization of the non-deterministic processes. And after all, we realize that state descriptions, which are the goal of our attempt, are not complete. How does an organism change over time (reduced to interval, and thus to numbers t ∈ R) brings up the quantum perspective, in the sense that we can no longer define the outcome of a complex process. Again, in Elsasser’s words: “The experimental method itself has a strong built-in bias in favor of stable results” [6, p. 143]. Therefore, we need to find ways to reflect the nomothetic dimension of the living through generalizations based on limiting assumptions (such as continuity), as well as the idiographic dimension of the organism (accounting for discreteness). The AnticipationScope is an attempt to reconcile the two by adding interactions to states and observables. This corresponds to the fact that anticipation is fundamentally expressed in interactions corresponding to adaptive dynamics. But while we know a lot about the interac- 4Reversible as applied to computation refers to a data processing implementation that is time-invertible. Living computation. tion of particles, we know very little about interactions characteristic of the living. Therefore, the AnticipationScope needs to evolve as a quantifying platform of interacting organisms (of individuals, in particular). At that level, risk emerges as related to interactions.
To interact means that the entities involved in the interaction evaluate observables on each other. It is not a reciprocal (or multi-) measurement, but rather an extraction of features based on which patterns are naturally recognized. In interactions, the interacting entities (cells, organs, organisms) “look” at each other in totally different ways than an observer looks at each and at their interaction. The complex behavior in the realm of the living is the outcome of interactions. In respect to the human being, this is almost a truism. But interactions evince also forms of risk that are simply not detectable at the level of the individual.
In recent months (February 2007, Pioneer Award Application), I suggested that the anticipation perspective opens an avenue towards risk evaluation in the extremely sensitive area of neurological disorders. As already pointed out, the AnticipationScope produces a record of how anticipatory characteristics underlying our adaptive capabilities change over time – the Anticipatory Profile™. Variations in the Anticipatory Profile are indicative of the individual’s adaptive capabilities. Disease or aging can affect the values. Accordingly, the AnticipationScope could help us identify the earliest onset of conditions that today are diagnosed only when they become symptomatic – usually years later (in the case of Parkinson’s disease, six years later). Delayed diagnosis (even of autism, despite its early onset) has negative consequences on the ability to assist those affected in a timely and effective manner. We probably also miss important information that might guide us in becoming proactive, as well as in finding a cure in some cases. To return to the example of Parkinson’s disease: festination (loss of the center of gravity adaptive performance, eventually resulting in “running steps”) could be revealed early through the Anticipation Scope. Using data gathered from one sensor at a time – such as practiced in describing, incompletely, ataxia, hemiparesis, dyskinesia, etc. – is a reductionist approach, useful but incomplete. Opposed to this is the integration of data from multiple sensors and from the motion capture that describes movements. This is the only way to capture the integrated nature of anticipation. In addition to specialized knowledge, we gain a holistic understanding of the affected human being. The human being is a relational entity – while each component is relevant, the outcome is not reducible to the function of one or another part of our body, but rather to their interrelationship, how they synchronize.
8. Structural measurement process
Actually, the basic premise of the entire design of the Anticipation Scope is derived from the knowledge gained in recent years through single-neuron recordings [12] on the unity between action and perception. Brain activity is specific to the task embodied in the goal, not to the particular effectors. When an object is grasped, neurons are activated regardless of the hand (left or right) or of the toes (left or right foot) that might be used, or even if the mouth is used. Purpose drives the action. Anticipation is always purpose related. Gallese [11] brings this observation to a clear point: “the object representation is integrated with the action simulation”. This broad understanding of the unity of perception, activation processes, control mechanisms, and the motoric will guide the realization of the AnticipationScope as a space of interaction between the subject of inquiry and objects associated with actions. Measurement within the AnticipationScope is goal related, since anticipations are always in respect to the outcome of an action. It has already been discussed herein that anticipation is not prediction, i.e., not a probabilistic process, but rather one driven by the evaluation of possibilities. The congenial perspective of the vast amounts of data collected (a variety of interactively selectable time correlated streams) is that of structural measurement process. The biologically inspired Evolving Transformation System (ETS) is the mathematical foundation for the structural measurement process [15]. ETS is a dynamic record of the interaction of elements involved in the functioning of a system, better yet in its self-organization. Each time we are involved in an action, learning takes place. The result is what we call experience.
8.1. Patterns of risk. Patterns of anticipation
The classes of risk pertinent to the physical (Class A), the living (Class B), and the artificial (Class C) are in some way connected to risk patterns (deterministic path, non-deterministic path, hybrid path). Pattern recognition, as a distinct mathematical representation, and its computational form are very efficient in respect to Class A risk. At the foundation of such pattern recognition processes, we certainly recognize inductive learning and the associated representation. As we know, it all boils down to defining a function g(x) :R^d{1, 2, . . . ,M}, which represents one’s guess (some give it fancier names) of y given x. The problem at hand is how we arrive at a good description of g, either in natural language, or in some other forms of expression preferable in mathematical descriptions that are computable. The mapping is called a classifier, which guides those in the business of assessing risk (engineers, insurance experts, etc.) in their decisions. For Class B risk, things are a bit more complicated. The risk associated with returning a fast tennis serve, for example, can affect the game’s outcome and the player’s reputation (read: lucrative endorsement contracts). The risk of falling during an Olympic or international downhill ski competition encapsulates many components: injury, lost victory, a blot on the skier’s record, etc. In this pattern description of risk, we tend to regard those who perform well – tennis players, skiers, chess players, as well as physicians and meteorologists – as having built-in classifiers. Given the enormous size of the space x, classifiers end up being anything but perfect. For those who play tennis and those who ski guided by reaction, i.e., below the anticipation threshold, where reaction defines interaction, pattern recognition is a very powerful method for guiding them towards higher performance. This is the type of machine simulation of the real event that can reach good predictive performance.
However, if the interaction between the living systems described above is over the threshold of reaction, we will probably have to work with dynamic pattern recognition. Let us shortly observe that dynamic is a relative qualifier. Some will define probabilistic-driven pattern recognition [4] as dynamic. The observation in such systems ends up being a d-dimensional vector x; the unknown nature of the observation is called class; and what stands as a substitute for inductive learning is the frequency of encountering some pairs of x and y in a relation that can be formalized. For the dynamic pattern recognition, experts no longer work on producing classifiers. They bring history (or ontologies) to the AI programmers – data from the past that evinces some pattern. That this is not formative history, which is Goldfarb’s subject, is obvious. Bayes classifiers work like that. Statistical pattern recognition belongs to the same perspective (one can use, as we know, Hidden Markov Models, which are a particular case of a stochastic finite state automaton). In other cases, such as when evolutionary natural objects were considered [32], fuzzy Petri Nets were used. I brought up these examples of what the pattern recognition community calls dynamic pattern recognition in order to make clear the dynamics referred to is well understood as pertaining to the deterministic domain. Risk assessment within such a domain is a relatively successful activity. That Class B risk is approached using means of analysis characteristic of Class A is, in fact, a reductionist approach.
Goldfarb, who wants to transcend the limitations of measurement expressed through numbers, is fully aware of these dynamic models. He is also inclined to integrate in his representation knowledge resulting from a stochastic perspective (ultimately, also captive to numbers).Without suggesting that the epistemological view promoted by Goldfarb is wrong or inadequate, I would like to suggest that, in addition to the inductive process, abductions, or hypothesis-driven learning, would have to be considered. There is no reason to doubt that Goldfarb can accommodate the need to account for abduction. Up to 1865, the common understanding in logic was that the so-called class of deductive arguments (also known as necessary inference), and the inductive arguments (probable inferences) covered the entire gamut. With Peirce [24], the class of probable inferences was further distinguished as inductive and abductive inferences (which he called hypotheses and retroductive inferences).
The suggestion I make at this time might prove beneficial for maintaining the goal of a unified representational system, which is Goldfarb’s goal. What abduction might supplant is the specific information that distinguishes the physical from the living, and both from the artificial endowed with characteristics of the living, without denying the implicit realization of the biological in the material substratum. Goldfarb might find his own ways to account for the distinction, not to say for associating to pattern recognition, in its classical formulation, a complementary focus: dynamic recognition driven by data that associates probability and possibility. Or, in another formulation, the complementary focus on risk (chanced outcome) and anticipation (outcome-driven action).
8.2. Dynamics of anticipation
We can examine anticipatory expression from the perspective of pattern recognition, or of dynamic systems – where anticipation looks like an attractor. We can consider anticipation as reverse computation – since in the living, the laws of thermodynamics need to be understood according to the condition of the living as an open system (metabolism dictates that energy be continuously taken in). We can think of anticipation as an expression of entanglement, though not at a quantum scale. What we cannot do is avoid considering the dynamics of anticipation, how it changes over time. In other words, can it be that we are born with it, or is anticipation the product of nurture, i.e., of learning? The dynamics of anticipation is the record of its evolutionary and developmental change. Both dimensions are of interest to a structural representation. The change in anticipatory characteristics over the life of the living entity under consideration is part of its coming into being and its eventual death. In many ways, it is the formative history of such an entity, and in this sense, ETS is not only a good candidate in providing a representation, but a test case for our ability to gain knowledge about anticipation. Such knowledge will eventually inform much of the science and technology of our age. We have already learned a lot about the brain activity of the young during their “explosive” hormonal phase; and we have learned quite a deal about how aging affects adults, that is, our anticipation. Adaptive capabilities being the result of anticipation at work, the failure to adapt is a risk resulting from inadequate anticipation.
Awareness of anticipation dates probably way back to questions asked about some individuals outperforming others in a context of “all things being equal”. I would prefer not to speculate on how this awareness is reflected in all kinds of descriptions. Survival implies anticipation, without excluding risk (as challenge). Let me succinctly point to two aspects: pregnancy, for instance, triggers increased anticipation [30], expressed in increased activity in the cingulated cortex. Recent data [17] documents that pregnant rats are more effective, by a factor of 6, than virgin rats in navigating mazes and in capturing prey. Pregnancy is risky (even under the best of circumstances), but the wager is against survival of the species, not individual performance. In contrast to pregnancy as an expression of enhanced anticipation, aging results in diminished anticipation (see Fig. 6). There is learning, inductive and abductive in nature, and loss of anticipation, each to be properly represented. As anticipation decreases, the risks associated with living increase (cf. [22,23]).
For example, the anticipatory baroreflex decreases [3]. Older individuals get dizzy when getting up (even from a chair), and when the atmospheric pressure changes [1]. This very often leads to a predisposition to stay in bed or to sit for longer periods of time, to passive habits (such as watching TV), and to avoid moving around. In such cases, activity is erroneously associated with dizziness, and a vicious, downward cycle begins. This is where we want to introduce forms of activity that will target the Anticipatory Profile. More precisely, we want to build upon brain plasticity in order to stimulate the cognitive “rejuvenation” of aging individuals. This is the project of the antÉ– Institute for Research in Anticipatory Systems entitled Seneludens (from Latin senex, to grow old; ludens, playful), best described as an attempt to minimize the various risks that arise from aging.
References
[1] H. Aikman, The association between arthritis and the weather, International Journal of Biometeorology 40(4) (1997), 192– 199.
[2] A. Bechara, A.R. Damasio, H. Damasio and S.W. Anderson, Insensitivity to future consequences following damage to human prefrontal cortex, Cognition 50 (1994), 7–15.
[3] A.J. Bowman, R.H. Clayton, A. Murray, J.W. Reed, M.F. Subhan and G.A. Ford, Baroreflex function in sedentary and endurance-trained elderly people, Age and Ageing 26 (1997), 221–224.
[4] L. Devroye, L. Györfy and G. Lugosi, A Probabilistic Theory of Pattern Recognition, Springer, New York/Heidelberg, 1996.
[5] D. Dorsey, Brain-driven Computer Game, The Sun Herald, March 18, 2007.
[6] W. Elsasser, Reflections on the Theory of Organisms. Holism in Biology, Johns Hopkins University Press, Baltimore, 1998. (Originally published in 1987 by ORBIS Publishing, Frelighsburg, Quebec.)
[7] R.P. Feynman, The Feynman Lectures on Computation, A.J.G. Hey and R.W. Allen, eds, Addison Wesley, Reading, 1996.
[8] R.P. Feynman, Feynman and Computation, A.J.G. Hey, ed., Perseus Books, Reading, 1998.
[9] M.S. Fischler and O. Firschein, Intelligence: The Eye, the Brain, and the Computer, Addison Wesley, Reading, 1987.
[10] Y. Gahery, Associated movements, postural adjustments and synergy: some comments about the history and significance of three motor concepts, Archives Italiennes de Biologie 125 (1987), 345–360.
[11] V. Gallese, The inner sense of action, Journal of Consciousness Studies 7(10) (2000), 23–40.
[12] M. Gentilucci, L. Fogassi, G. Luppino, M. Matelli, R. Camarada and G. Rizzolatti, Functional organization of inferior area 6 in the macaque monkey: I. Somatotopy and the control of proximal movements, Experimental Brain Research 71 (1988), 475–490.
[13] K. Gödel, Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, Monatshefte für Mathematik und Physik 38 (1931), 173–198.
[14] L. Goldfarb, D. Gay, O. Golubitsky and D. Korkin, What is a structural representation?, variation 6, updated October 27, 2006; http://www.cs.unb.ca/~goldfarb/ ETS_special_issue/ETS5.pdf.
[15] L. Goldfarb and O. Golubitsky, What is a structural measurement process?, Faculty of Computer Science, University of New Brunswick, Canada, November 30, 2001; http://www.cs. unb.ca/~goldfarb/smp.pdf.
[16] L. Goldfarb, O. Golubitsky and D. Korkin, What is a structural representation?, Technical Report TR00-137, Faculty of Computer Science, UNB, 2000.
[17] C.H. Kinsley and K.G. Lambert, The maternal brain, Scientific American 294 (2006), 72–79.
[18] F. Knight, Risk, Uncertainty, and Profit, Hart, Schaffner & Marx (Houghton Mifflin Company), Boston, 1921.
[19] M. Nadin, Mind – Anticipation and Chaos, Belser Verlag, Stuttgart/Zurich, 1991.
[20] M. Nadin, Anticipation – The End Is Where We Start From, Lars Mueller Verlag, Basel, 2003.
[21] M. Nadin, Not everything we know we learned, in: Adaptive Behavior in Anticipatory Learning Systems, LNAI, Vol. 2684, Bertelsmann–Springer, Heidelberg, 2003, pp. 23–43.
[22] M. Nadin, G.N. Pradhan, N. Engineer and B. Prabhakaran, Analyzing motoric and physiological data in describing upper extremity movement in the aged, ACM International Conference Proceeding Series 282 (2008).
[23] M. Nadin, G.N. Pradhan, N. Engineer and B. Prabhakaran, An integrated mobile wireless system for capturing physiological data streams during a cognitive-motor task: Applications for aging, in: Engineering in Medicine and Biology Workshop, 2007, IEEE, Dallas, 2008, pp. 67–70.
[24] C.S. Peirce, The Collected Papers of Charles Sanders Peirce, Vols 1–6, C. Hartshorne and P. Weiss, eds, Harvard University Press, Cambridge, MA, 1931–1935, CP 1:74.
[25] M.S. Pini, F. Rossi and B. Venable, Possibilistic and probabilistic uncertainty in soft constraint problems, Quantitative Approaches to Reasoning and Uncertainty 3571 (2005), 800–811.
[26] K. Popper, The Logic of Scientific Discovery, Basic Books, New York, 1959.
[27] R. Rosen, Foundations of Mathematical Biology, Vol. 2, Academic Press, New York/London, 1972.
[28] R. Rosen, On the dynamical realization of (M, R) systems, Bulletin of Mathematical Biology 35 (1973), 1–9.
[29] R. Rosen, Anticipatory Systems. Philosophical, Mathematical, and Methodological Foundations, Pergamon Press, London, 1985.
[30] J.A. Russell, A.J. Douglas, R.F.Windle and C.D. Ingram (eds), The Maternal Brain: Neurobiological and Neuroendocrine Adaptation and Disorders, Preganancy and Post-Partum, Elsevier, Dordrecht, 2001.
[31] A. Tarantola, Popper, Bayes, and the inverse problem, Nature – Physics 2 (2006), 492–494.
[32] G.P. Veyis, P. Loomis and M. Menard, A Fuzzy Petri Net for pattern recognition: Application to dynamic classes, Knowledge and Information Systems 4(1) (2002), 112–128.
[33] A. Wildavski, Searching for Safety, Transactions Publishers, New Brunswick, USA, 1988.
[34] W. Windelband, Geschichte und Naturwissenschaft, 1894 (see Strassburger Rektoratsrede: http://www.fh-augsburg.de/ ~harsch/germanica/Chronologie/19Jh/Windelband/win_rede. html).
[35] L.A. Zadeh, Fuzzy sets, Information and Control 8 (1965), 338–353.
[36] L.A. Zadeh, Fuzzy sets as a basis for a theory of possibility, Fuzzy Sets and Systems 1 (1978), 3–28.
[37] L.A. Zadeh, PRUF – a meaning representation language for natural languages, International Journal of Man–Machine Studies 10 (1978), 395–460.